tìm các giá trị nguyên của x để P=x2/x-1 nhận giá trị nguyên
tìm GTNN của P=x2/x-1 khi x>1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c) Để A nhận giá trị nguyên khi và chỉ khi:
![]()
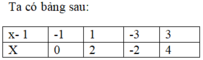
Kết hợp với điều kiện, tập hợp các giá trị của x nguyên để A nguyên là: {0; 2; -2; 4}.

Bài 1:
a) Ta có: \(P=1+\dfrac{3}{x^2+5x+6}:\left(\dfrac{8x^2}{4x^3-8x^2}-\dfrac{3x}{3x^2-12}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{8x^2}{4x^2\left(x-2\right)}-\dfrac{3x}{3\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\left(\dfrac{4}{x-2}-\dfrac{x}{\left(x-2\right)\left(x+2\right)}-\dfrac{1}{x+2}\right)\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}:\dfrac{4\left(x+2\right)-x-\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=1+\dfrac{3}{\left(x+2\right)\left(x+3\right)}\cdot\dfrac{\left(x-2\right)\left(x+2\right)}{4x+8-x-x+2}\)
\(=1+3\cdot\dfrac{\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=1+\dfrac{3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{\left(x+3\right)\left(2x+10\right)+3\left(x-2\right)}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+10x+6x+30+3x-6}{\left(x+3\right)\left(2x+10\right)}\)
\(=\dfrac{2x^2+19x-6}{\left(x+3\right)\left(2x+10\right)}\)

Bài 8:
\(F=x^2-2x+1+x^2-6x+9=2x^2-8x+10\\ F=2\left(x^2-4x+4\right)+2=2\left(x-2\right)^2+2\ge2\\ F_{min}=2\Leftrightarrow x=2\)
Bài 9:
\(A=-x^2+2x-1+5=-\left(x-1\right)^2+5\le5\\ A_{max}=5\Leftrightarrow x=1\\ B=-x^2+10x-25+2=-\left(x-5\right)^2+2\le2\\ B_{max}=2\Leftrightarrow x=5\\ C=-x^2+6x-9+9=-\left(x-3\right)^2+9\le9\\ C_{max}=9\Leftrightarrow x=3\)

Bài 1:
a: \(x^2+5x=x\left(x+5\right)\)
Để biểu thức này âm thì \(x\left(x+5\right)< 0\)
hay -5<x<0
b: \(3\left(2x+3\right)\left(3x-5\right)< 0\)
\(\Leftrightarrow-\dfrac{3}{2}< x< \dfrac{5}{3}\)

ĐKXĐ: x>=0
Để P là số nguyên thì \(\sqrt{x}+2⋮\sqrt{x}+1\)
=>\(\sqrt{x}+1+1⋮\sqrt{x}+1\)
=>\(\sqrt{x}+1\inƯ\left(1\right)\)
=>\(\sqrt{x}+1=1\) hoặc \(\sqrt{x}+1=-1\)
=>x=0(nhận) hoặc \(\sqrt{x}=-2\)(loại)
\(P=\dfrac{\sqrt{x}+1+1}{\sqrt{x}+1}=1+\dfrac{1}{\sqrt{x}+1}\)
\(\sqrt{x}+1>=1\)
=>\(\dfrac{1}{\sqrt{x}+1}< =1\)
=>\(\dfrac{1}{\sqrt{x}+1}+1< =2\)
=>P<=2 với mọi x thỏa mãn ĐKXĐ
Dấu = xảy ra khi x=0

Phân thức 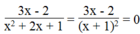 khi 3x – 2 = 0 và
x
+
1
2
≠
0
khi 3x – 2 = 0 và
x
+
1
2
≠
0
Ta có: x + 1 2 ≠ 0 ⇔ x + 1 ≠ 0 ⇔ x ≠ - 1
3x – 2 = 0 ⇔ 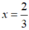
Ta có: 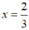 thỏa mãn điều kiện x
≠
- 1
thỏa mãn điều kiện x
≠
- 1
Vậy 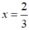 thì phân thức
thì phân thức 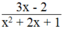 có giá trị bằng 0.
có giá trị bằng 0.
đề bài ĐKXĐ như nào bạn tự xét gtri thỏa mãn nhé
\(P=\frac{x^2}{x-1}=\frac{x^2-x+x-1+1}{x-1}=\frac{x\left(x-1\right)+\left(x-1\right)+1}{x-1}=x+1+\frac{1}{x-1}\)
Vì x nguyên nên x + 1 nguyên
Để P nguyên thì 1/x-1 nguyên ( đến đây quá dễ rồi:)) )
Như trên ta có : \(P=x+1+\frac{1}{x-1}=\left[\left(x-1\right)+\frac{1}{x-1}\right]+2\)
Vì x > 1, áp dụng bất đẳng thức AM-GM ta có :
\(P\ge2\sqrt{\left(x-1\right)\cdot\frac{1}{x-1}}+2=4\). Đẳng thức xảy ra <=> x = 2
Vậy GTNN của P = 4 <=> x=2