Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)
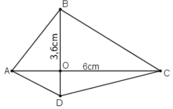
Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài. Chẳng hạn tứ giác ABCD ở hình trên.
Ta có: AC = 6cm, BD = 3,6cm và AC ⊥ BD.
Diện tích tứ giác ABCD là:
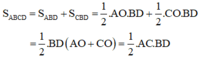
Mà AC = 6cm ; BD = 3,6 cm nên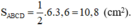 
b) Hình vuông có 2 đường chéo vuông góc nên theo công thức trên, diện tích của nó là: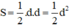 
a) Học sinh tự vẽ tứ giác thỏa mãn điều kiện đề bài, chẳng hạn như tứ giác ABCD ở hình dưới có
AC = 6cm
BD = 3,6cm
AC BD
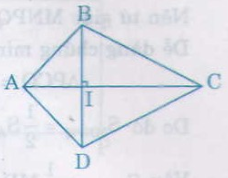
Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài:
AC = 6cm
BD = 3,6cm
AC BD tại I với I là điểm tùy ý thuộc đoạn AC và BD
Diện tích củ tứ giác vừa vẽ:
SABCD = AC. BD = 6. 3,6 = 10,8 (cm2)
b) Diện tích hình vuông có độ dài đường chéo là d
Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau, nên diện tích là:
S = d.d = d2
tứ giác ABCD ở hình dưới có
AC = 6cm
BD = 3,6cm
AC BD
Có thể vẽ được vô số tứ giác theo yêu cầu từ đề bài:
AC = 6cm
BD = 3,6cm
AC BD tại I với I là điểm tùy ý thuộc đoạn AC và BD
Diện tích củ tứ giác vừa vẽ:
SABCD = AC. BD = 6. 3,6 = 10,8 (cm2)
b) Diện tích hình vuông có độ dài đường chéo là d
Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau, nên diện tích là:
S = d.d = d2
diện tích hình thoi là: (đổi 5m= 50 dm)
\(\dfrac{50\cdot20}{2}\) = 500(dm)
diện tích hình thoi ABCD là:
\(\dfrac{8\cdot6}{2}\) =24(cm)
Diện tích của hình thoi là: 6 .8 : 2 = 24 cm^2
Cạnh của hình thoi là: \(\sqrt{\left(\frac{6}{2}\right)^2+\left(\frac{8}{2}\right)^2}=5\) cm
Chiều cao của hình thoi là: 24 : 5 = 4,8 cm
Vậy:...
Câu 11:
Xét ΔABC và ΔMNP có
\(\dfrac{AB}{MN}=\dfrac{AC}{MP}=\dfrac{BC}{NP}\left(=\dfrac{1}{2}\right)\)
Do đó: ΔABC~ΔMNP
Câu 12:
a: Xét ΔAMC và ΔANB có
\(\dfrac{AM}{AN}=\dfrac{AC}{AB}\left(\dfrac{10}{8}=\dfrac{15}{12}\right)\)
\(\widehat{MAC}\) chung
Do đó: ΔAMC đồng dạng với ΔANB
b: Ta có: ΔAMC đồng dạng với ΔANB
=>\(\widehat{ACM}=\widehat{ABN}\)
Xét ΔHMB và ΔHNC có
\(\widehat{HBM}=\widehat{HCN}\)
\(\widehat{MHB}=\widehat{NHC}\)(hai góc đối đỉnh)
Do đó; ΔHMB đồng dạng với ΔHNC
=>\(\dfrac{HB}{HC}=\dfrac{BM}{CN}\)
=>\(HB\cdot CN=BM\cdot CH\)
Câu 10:
Xét ΔOAD và ΔOCB có
\(\dfrac{OA}{OC}=\dfrac{OD}{OB}\)
góc O chung
Do đó: ΔOAD~ΔOCB
DBDC, viết các cặp góc tương ứng bằng nhau của hai tam giác đã cho. 
có AB = 3cm, AC = 4,5cm, BC = 6cm. 
có DE= 12cm, EF=9cm, DF = 6cm. Chứng minh 
. 
AC). Tính AN? 
nhọn. Trên cạnh Ox, đặt các đoạn thẳng OA = 6cm, OB = 18cm. Trên cạnh Oy, đặt các đoạn thẳng OC = 9cm, OD = 12cm.Chứng minh hai tam giác OAD và OCB đồng dạng. 
có 
và 
có MN = 6cm; MP = 8cm; 
đồng dạng với 
