Cho hai đường tròn (O) và (O’) cắt nhau tại hai điểm A và B. Gọi EF là một tiếp tuyến chung của
chúng (E; F là các tiếp điểm) và AB cắt EF tại I.
a) Chứng minh hai tam giác IEA và IBE đồng dạng.
b) Chứng minh I là trung điểm của EF.
c) Gọi C là điểm đối xứng với B qua I. Chứng minh tứ giác AECF nội tiếp đường tròn.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: TH1: A và CD nằm cùng một phía so với đường O'O
góc ABC=góc AEC=góc ICD
góc DBC=gsoc AED=góc IDC
=>góc DBA+góc DIC=góc ABC+góc DBC+góc DIC
=góc ICD+góc IDC+góc DIC=180 độ
=>BCID nội tiếp
TH2: A và CD nằm khác phía so với O'O
ABCE nội tiếp (O)
=>góc BCE+góc BAE=180 độ
=>góc BCE=góc BAF
Tương tự, ta được: góc BAF=góc BDI
=>góc BCE=góc BDI
=>góc BCI+góc BDI=180 độ
=>BCID nội tiếp
b: góc ICD=góc CEA=góc DCA
=>góc ICD=góc DCA
Chứng minh tương tự, ta được: góc IDC=góc CDA
Xét ΔICD và ΔACD có
góc ICD=góc DCA
CD chung
góc IDC=góc CDA
=>ΔICD=ΔACD
=>DI=DA và CI=CA
=>CD là trung trực của AI
c:
CD vuông góc AI
=>AI vuông góc MN
Gọi K là giao của AB và CD
Chứng minh được CK^2=KA*KB=KD^2
=>KC=KC
CD//MN
=>KC/AN=KD/AM=KB/AB
=>AN=AM
=>ΔIMN cân tại I
=>IA là phân giác của góc MIN

Đường tròn có đường kính BC có tâm M, bán kính MA.OO' vuông góc với MA tại A nên là tiếp tuyến của đường tròn (M).

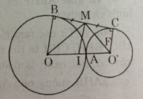
Gọi I là trung điểm của OO', I là tâm của đường tròn có đường kính OO', IM là bán kính (vì MI là trung tuyến ứng với cạnh huyền của MOO'. IM là đường trung bình của hình thang OBCO' nên IM // OB // O'C. Do đó IM ⊥ BC.
BC vuông góc với IM tại M nên BC là tiếp tuyến của đường tròn (I).
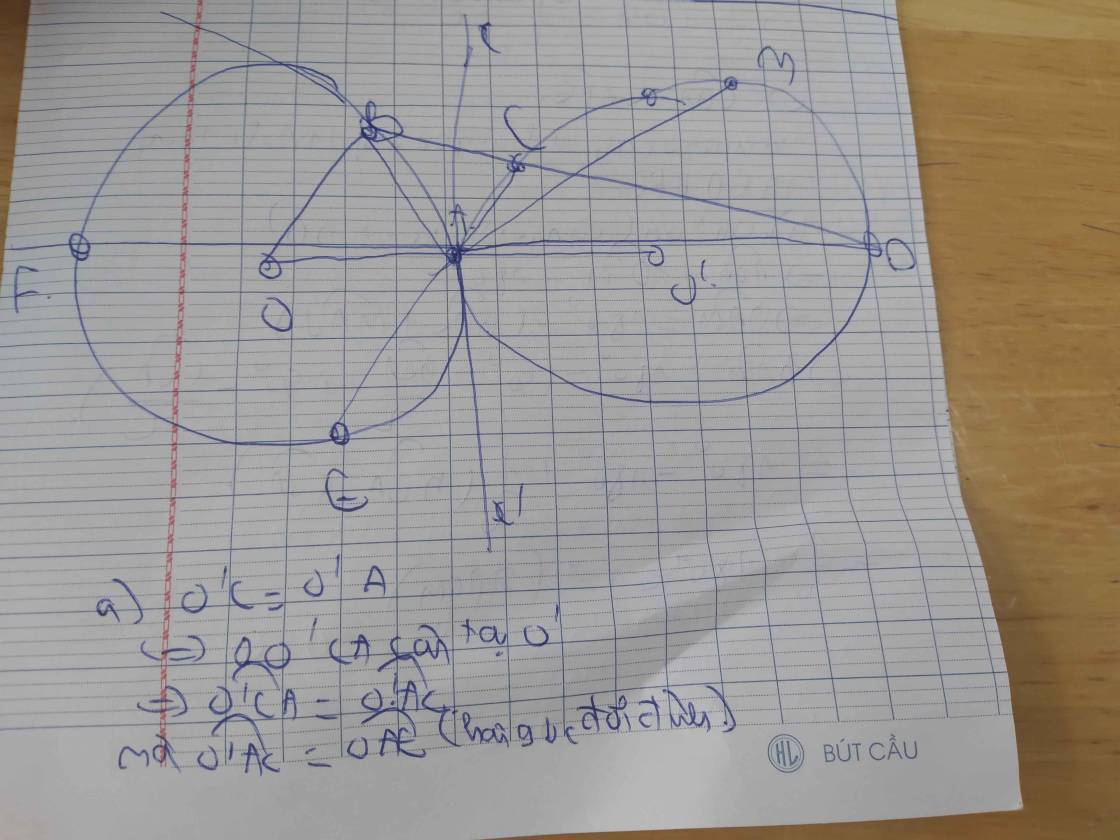


a: Xét (O) có
\(\widehat{IEA}\) là góc tạo bởi tiếp tuyến EI và dây cung EA
\(\widehat{ABE}\) là góc nội tiếp chắn cung AE
Do đó: \(\widehat{IEA}=\widehat{ABE}\)
Xét ΔIEA và ΔIBE có
\(\widehat{IEA}=\widehat{IBE}\)
\(\widehat{EIA}\) chung
Do đó: ΔIEA đồng dạng với ΔIBE
b: Xét (O') có
\(\widehat{IFA}\) là góc tạo bởi tiếp tuyến FI và dây cung FA
\(\widehat{FBA}\) là góc nội tiếp chắn cung FA
Do đó: \(\widehat{IFA}=\widehat{FBA}\)
Xét ΔIFA và ΔIBF có
\(\widehat{IFA}=\widehat{IBF}\)
\(\widehat{FIA}\) chung
Do đó: ΔIFA đồng dạng với ΔIBF
=>\(\dfrac{IF}{IB}=\dfrac{IA}{IF}\)
=>\(IF^2=IB\cdot IA\)
ΔIEA đồng dạng với ΔIBE
=>\(\dfrac{IE}{IB}=\dfrac{IA}{IE}\)
=>\(IE^2=IA\cdot IB\)
=>IE=IF
=>I là trung điểm của EF