Chứng minh trog hthag các tia phân giác của 2 góc kề 1 cạnh bên vuông góc với nhau
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
12 tháng 8 2017
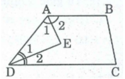
Giả sử hình thang ABCD có AB // CD
* Ta có: ∠ A 1 = ∠ A 2 = 1/2 ∠ A (vì AE là tia phân giác của góc A)
∠ D 1 = ∠ D 2 = 1/2 ∠ D ( Vì DE là tia phân giác của góc D)
Mà ∠ A + ∠ D = 180 0 (2 góc trong cùng phía bù nhau)
Suy ra: ∠ A 1 + ∠ D 1 = 1/2 ( ∠ A + ∠ D) = 90 0
* Trong ΔAED, ta có:
∠ (AED) + ∠ A 1 + ∠ D 1 = 180 0 (tổng 3 góc trong tam giác)
⇒ ∠ (AED) = 180 0 – ( ∠ A 1 + ∠ D 1 ) = 180 0 - 90 0 = 90 0
Vậy AE ⊥ DE.
R
0
29 tháng 6 2017
nên \(\widehat{A}_1+\widehat{D}_1=90^0\). \(\Delta ADE\) có \(\widehat{A}_1+\widehat{D}_1=90^0\) nên \(\widehat{AED}=90^0\). Vậy \(AE\perp DE\)
T
2 tháng 9 2018
Giải sử hình thang ABCD có AB// CD
\(\widehat{A_1}=\widehat{A_2}=\dfrac{1}{2}\widehat{A}\left(gt\right)\)
\(\widehat{D_1}=\widehat{D_2}=\dfrac{1}{2}\widehat{D}\left(gt\right)\)
Mà \(\widehat{A}+\widehat{D}=180^o\) (hai góc trong cùng phía bù nhau)
Suy ra:
\(\widehat{A}_1+\widehat{D_1}=\dfrac{1}{2}\left(\widehat{A}+\widehat{D}\right)=\dfrac{1}{2}.180^o=90^o\)
Trong ∆ AED ta có :
\(\widehat{AED}+\widehat{A_1}+\widehat{D_1}=180^o\) (tổng ba góc trong 1 tam giác)
\(\Rightarrow\widehat{AED}=180^o-\left(\widehat{A_1}+\widehat{D_1}\right)=180^o-90^o=90^o\)
\(\Rightarrow AE\perp ED\)
Vậy trong hình thang các tia phân giác của hai góc nhọn kề một cạnh bên vuông góc với nhau
QM
2
27 tháng 6 2015
Gọi ht đó là ABCD nha , AE là phân giác A ; DE là phân GIÁC cắt nhau tại E
AB //CD => A + D = 180 ĐỘ
Ta có EAD = 1/2 A (AE là phân giác ) (2)
EDA = 1/2 D ( DE là phân giác ) (1)
Từ (1) và (2) => EAD + EDA = = 1/2 ( A + D ) = 1/2.180 = 90 độ
TAM giác EAD có EAD + EDA = 90 độ => AED = 90độ
Hay AE vuông góc với DE
Tương tự cm với tia phân giác B và C
27 tháng 6 2015
Ta gọi góc vuông là O .
Kéo dài CO sao cho CO=OE.
Kéo dài DO sao cho DO=OF
Xét tam giác DOC và tam giác EOF có :
CO=OE(cmt)
DO=OF(cmt)
O1=O2(đđ)
=>tam giác DOC+tam giác EOF = 360 độ
Mà 2 tam giác cân=> 2 tam giác = 360độ =>O=E+F+D1+C1:2=>góc O:2=90 độ
29 tháng 8 2016
1 )
Xét hình thang ABCD (AB//CD)
góc A + góc D =180 độ (2 góc trong cùng phía )
góc B +góc C =180 độ
- Nếu góc A tù (> 90độ) => góc D nhọn
- Nếu góc B tú => góc C nhọn
=> hình thang có nhiều nhất 2 góc tù, có nhiều nhất 2 góc nhọn
2 ) Giả sử ABCD là hình thang có đáy AB//CD
Khi đó ta có góc A + góc D bằng 180 độ (2 góc kề 1 cạnh bên hình thang bù nhau) (Hoặc bạn hiểu là 2 góc trong cùng phía bù nhau đó)
Vậy tia phân giác góc A nên bằng nửa góc A
TIa phân giác góc D bằng nửa góc D
Vậy Cộng 2 góc tia phân giác đó bằng 180độ chia 2 bằng 90 độ
29 tháng 8 2016
2,
Giả sử ABCD là hình thang có đáy AB//CD
Khi đó ta có góc A + góc D bằng 180 độ (2 góc kề 1 cạnh bên hình thang bù nhau) (Hoặc bạn hiểu là 2 góc trong cùng phía bù nhau đó)
Vậy tia phân giác góc A nên bằng nửa góc A
TIa phân giác góc D bằng nửa góc D
Vậy Cộng 2 góc tia phân giác đó bằng 180 độ chia 2 bằng 90 độ
5 tháng 9 2016
Gọi góc xOz, góc zOy là 2 góc kề bù ; và tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy.
o
* Để chứng minh 2 tia phân giác của 2 góc kề bù vuông góc với nhau, ta sẽ chứng minh tia Ou vuông góc tia Ov.
* Vì tia Ou, Ov lần lượt là tia phân giác của góc xOz, zOy
nên:
{ góc uOz = 1/2 góc xOz
{ góc zOv = 1/2 góc zOy
Suy ra:
{ 2 góc uOz = góc xOz
{ 2 góc zOv = góc zOy
Ta lại có:
góc xOz + góc zOy = 180 độ (vì 2 góc xOz, góc zOy kề bù)
=> 2 góc uOz + 2 góc zOv = 180 độ
=> 2(góc uOz + góc zOv) = 180 độ
=> góc uOz + góc zOv = 90 độ
=> góc uOv = 90 độ (vì 2 góc uOz, góc zOv kề nhau)
=> Tia Ou vuông góc Tia Ov
Do đó, 2 tia phân giác của 2 góc kề bù thì vuông góc với nhau.
E
2 tháng 4 2021
1,Cho 2 góc xOy và yOz kề bù .
Om ; On lần lượt là tia phân giác của 2 góc đó
⇒{ˆO1=ˆO2=12.ˆxOyˆO3=ˆO4=12.ˆyOz⇒{O1^=O2^=12.xOy^O3^=O4^=12.yOz^
⇒ˆO2+ˆO3=12(ˆxOy+ˆyOz)=12.1800=900⇒O2^+O3^=12(xOy^+yOz^)=12.1800=900
=> Đpcm
NB
3
19 tháng 5 2017
A = A1 + A2 = 2A1 = 2A2
D = D1 + D2 = 2D1 =2D2
mà A + D =180O => A1 +D1 = 90
Gọi 2 tia phân giac góc A và D cắt nhau tại K xet tg AKD có A+D = 90 => K =90 (dpcm)