Cho ΔABC = ΔMNP. Biết góc M bằng 45 độ, góc n bằng 65 độ. Tính số đo của góc C? giúp mình với ạaa :<
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


mk không vẽ hình nha ì hì:
a) Vì góc xOy và yOz là 2 góc kề nhau nên tia Oy nằm giữa 2 tia Ox và Oz
suy ra xOy + yOz=xOz
40 + 120 = xOz
suy ra xOz = 160 độ
b) Vì Ot là tia phân giác của góc xOz nên
xOt= xOz :2=160:2=80
Trên cùng 1 nửa mp bờ chứa tia Ox vì xOy < xOt ( 40 < 80 )
suy ra tia Oy nằm giữa 2 tia Ox và Ot(1)
suy ra xOy + yOt = xOt
40 + yot = 80
yot= 80-40=40 độ
Suy ra xoy=yot=40 độ(2)
c) Từ (1) và(2) suy ra tia Oy là tia phân giác của xOt
nhớ k cho mk nha
nếu sai sót thì mong bn đừng giận nha

a) Ta có tam giác MNP cân tại M => \(\widehat{N}=\widehat{P}\)
mà \(\widehat{M}+\widehat{N}+\widehat{P}=180^0\)
\(=>\widehat{N}+\widehat{P}=180^0-\widehat{M}=180^0-65^0=115^0\)
\(=>\widehat{N}=\widehat{P}=115^0:2=57,5^0\)
b) Ta có \(\widehat{N}=\widehat{P}\left(cmt\right)\)
\(=>\widehat{P}=50^0\)
Mà \(\widehat{M}+\widehat{N}+\widehat{P}=180^0\)
\(=>\widehat{M}=180^0-\left(\widehat{N}+\widehat{P}\right)=180^0-\left(50^0+50^0\right)=180^0-100^0=80^0\)

Ta sẽ giả sử tổng số đo 3 góc EOM,EON,FOM là 250 độ như đề bài yêu cầu
Cách 1:
Ta có: \(\widehat{EOM}+\widehat{EON}+\widehat{FOM}+\widehat{FON}=360^0\)
=>\(\widehat{FON}+250^0=360^0\)
=>\(\widehat{FON}=110^0\)
\(\widehat{FON}=\widehat{EOM}\)(hai góc đối đỉnh)
mà \(\widehat{FON}=110^0\)
nên \(\widehat{EOM}=110^0\)
\(\widehat{EOM}+\widehat{EON}=180^0\)(hai góc kề bù)
=>\(\widehat{EON}+110^0=180^0\)
=>\(\widehat{EON}=70^0\)
\(\widehat{EON}=\widehat{FOM}\)(hai góc đối đỉnh)
mà \(\widehat{EON}=70^0\)
nên \(\widehat{FOM}=70^0\)
Cách 2: \(\widehat{EON}=\widehat{FOM}\)(hai góc đối đỉnh)
=>\(\widehat{EON}+\widehat{FOM}=2\cdot\widehat{EON}\)
\(\widehat{EON}+\widehat{FOM}+\widehat{EOM}=250^0\)
=>\(2\cdot\widehat{EON}+\widehat{EOM}=250^0\)(2)
Ta lại có: \(\widehat{EON}+\widehat{EOM}=180^0\)(hai góc kề bù)(1)
nên từ (1),(2) ta sẽ có hệ phương trình:
\(\left\{{}\begin{matrix}2\cdot\widehat{EON}+\widehat{EOM}=250^0\\\widehat{EON}+\widehat{EOM}=180^0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2\cdot\widehat{EON}+\widehat{EOM}-\widehat{EON}-\widehat{EOM}=250^0-180^0=70^0\\\widehat{EON}+\widehat{EOM}=180^0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\widehat{EON}=70^0\\\widehat{EOM}=180^0-70^0=110^0\end{matrix}\right.\)
\(\widehat{EON}=\widehat{FOM}\)(hai góc đối đỉnh)
mà \(\widehat{EON}=70^0\)
nên \(\widehat{FOM}=70^0\)
\(\widehat{EOM}=\widehat{FON}\)(hai góc đối đỉnh)
mà \(\widehat{EOM}=110^0\)
nên \(\widehat{FON}=110^0\)
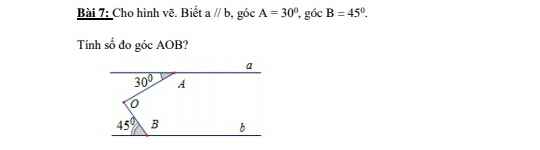
C=70o