Vẽ hình và giải giúp mình với 😭😭
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
1
MP
16 tháng 3 2021
a)xét tam giác KHF vuông tại H và tam giác AHF vuông tại H có
FH chung
KH=HA(gt)
=>tam giác KHF=tam giác AHF(2 cạnh góc vuông)
=>FK=FA(cạnh tương ứng)
b)Xét tam giác FMK và tam giác CMB có
FM=MC(M là trung điểm FC)
FMK=CMB(đối đỉnh)
KM=MB(gt)
=>tam giác FMK=tam giác CMB(c-g-c)
=>BC=FK(cạnh tương ứng)
mà FK=FA(câu a)
=>BC=FA
c) xét tam giác AKM có
HM vuông góc với AK(KH vuông góc với FC)
H là trung điểm AK(KH=AK)
=>tam giác AKM cân tại M(dhnb)
=>KM=AK(t/c)
mà M là trung điểm KB(MK=MB)
=>KM=AK=MB
=>tam giác KAB vuông tại A(trung tuyến thuộc cạnh huyền)
=>AB vuông góc với AK(t/c)
mà HM vuông góc với AK(gt)
=>HM//AB
hay FC//AB(đpcm)
16 tháng 3 2021
Câu 6:
a) Xét ΔABM vuông tại M và ΔACM vuông tại M có
AB=AC(ΔABC cân tại A)
AM chung
Do đó: ΔABM=ΔACM(Cạnh huyền-cạnh góc vuông)
16 tháng 4 2022
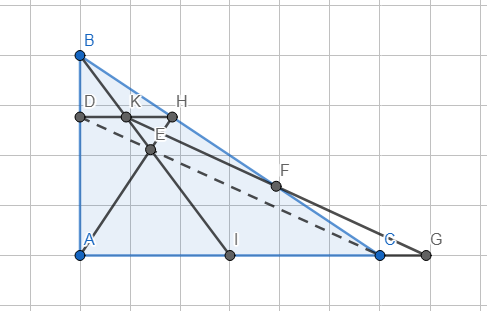
a. △ABH và △CBA có: \(\widehat{B}\) chung; \(\widehat{AHB}=\widehat{CAB}=90^0\).
\(\Rightarrow\)△ABH∼△CBA (g-g).
b. △ABI có: DK//AI (cùng vuông góc AB).
\(\Rightarrow\dfrac{DK}{AI}=\dfrac{BK}{BI}\)
△CBI có: KH//CI (cùng vuông góc AB).
\(\Rightarrow\dfrac{HK}{CI}=\dfrac{BK}{BI}=\dfrac{DK}{AI}\Rightarrow HK=DK\Rightarrow\)K là trung điểm DH.
c. Qua K kẻ đg thẳng song song DC cắt BC, AC tại F,G.
△HDC có: KF//DC, K là trung điểm DH \(\Rightarrow\)F là trung điểm HC.
\(\Rightarrow\)△KHF=△GCF (g-c-g) \(\Rightarrow KH=CG\).
△KHE có: KH//AI \(\Rightarrow\dfrac{KE}{EI}=\dfrac{KH}{AI}=\dfrac{CG}{CI}\Rightarrow\)EC//KG
\(\Rightarrow\)D,C,E thẳng hàng.
30 tháng 4 2022
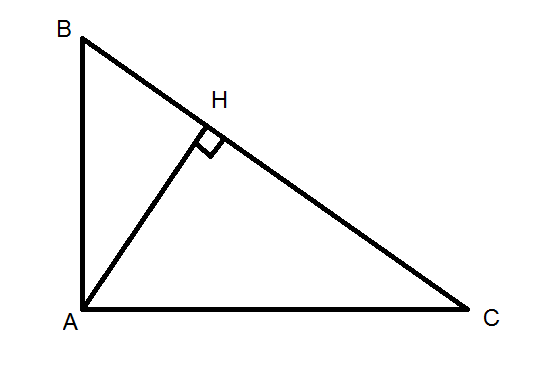
a: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)
Do đó: ΔHEB\(\sim\)ΔHDC
Suy ra: HE/HD=HB/HC
hay \(HE\cdot HC=HB\cdot HD\)
b: Xét ΔHED và ΔHBC có
HE/HB=HD/HC
\(\widehat{EHD}=\widehat{BHC}\)
Do đó: ΔHED\(\sim\)ΔHBC
Suy ra: \(\widehat{HED}=\widehat{HBC}\)
7 tháng 7 2023
a: Xét ΔBED vuông tại E và ΔBAC vuông tại A có
góc B chung
=>ΔBED đồng dạng với ΔBAC
b: Xét ΔCAB có FD//AB
nên CD/DB=CF/FA
=>DB/DC=FA/FC
16 tháng 4 2022
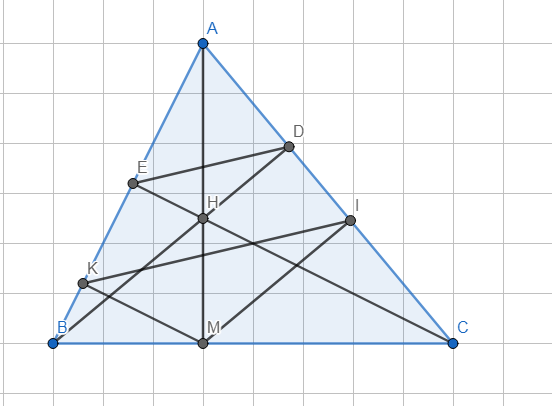
a) △ABC có: 2 đg cao BD và CE cắt nhau tại H.
\(\Rightarrow\)H là trực tâm △ABC mà AH cắt BC tại M.
\(\Rightarrow\)AM⊥BC tại M.
△AEC và △ADB có: \(\widehat{A}\) chung; \(\widehat{AEC}=\widehat{ADB}=90^0\)
\(\Rightarrow\)△AEC∼△ADB (g-g).
b) \(\Rightarrow\dfrac{AE}{AD}=\dfrac{AC}{AB}\Rightarrow\dfrac{AE}{AC}=\dfrac{AD}{AB}\)
\(\Rightarrow\)△AED∼△ACB (c-g-c).
c) Không hiểu đề cho điểm T làm gì?
\(\dfrac{AE}{EK}=\dfrac{AH}{HM}=\dfrac{AD}{DI}\Rightarrow\)KI//ED.
△AMK và △MBK có: \(\widehat{AKM}=\widehat{MKB}=90^0\); \(\widehat{AMK}=\widehat{MBK}\) (cùng phụ với \(\widehat{BMK}\))
\(\Rightarrow\)△AMK∼△MBK (g-g) \(\Rightarrow\dfrac{AK}{MK}=\dfrac{MK}{BK}\Rightarrow MK^2=AK.BK\)
△AMI và △MCI có: \(\widehat{AIM}=\widehat{MIC}=90^0\); \(\widehat{AMI}=\widehat{MCI}\) (cùng phụ với \(\widehat{CMI}\))
\(\Rightarrow\)△AMI∼△MCI (g-g) \(\Rightarrow\dfrac{AI}{MI}=\dfrac{MI}{CI}\Rightarrow MI^2=AI.CI\)
\(\left(AK^2+MK^2\right)+\left(AI^2+MI^2\right)=AM^2+AM^2=2AM^2\)
\(\Rightarrow AK^2+AI^2+AK.BK+AI.CI=2AM^2\)
hình
a) Xét tam giác ABD và tam giác ACE có :
góc ADB = góc AEC = 90 độ
góc A chung
=> tam giác ABD ~ tam giác ACE (g.g)
=> AD/AE = AB/AC (yttu)
=> AE.AB = AC.AD
Câu a)+b)