tìm x : (x4)2= x 12/x5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
6 tháng 7 2019
a) 4 , 5 − 2. x .1 4 7 = 11 14 ⇒ 4 , 5 − 2. x = 11 14 : 11 7 ⇒ 9 2 − 2. x = 1 2 ⇒ 2. x = 9 2 − 1 2 = 4 ⇒ x = 2.
b) x 4 − x 5 = − 1 1 2 ⇒ x . 1 4 − 1 5 = − 3 2 ⇒ x . 1 20 = − 3 2 ⇒ x = − 3 2 . 1 20 = − 3 40 .
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 3 2020
1.
a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)
\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)
\(\Leftrightarrow x^3+3x^2+2x-6=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)
b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)
\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 3 2020
1c/
\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)
\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)
\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn
Vậy pt có nghiệm duy nhất \(x=-1\)
CM
28 tháng 8 2019
Ta có:
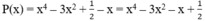
Vì : P(x) + Q(x) = x5 – 2x2 + 1
Suy ra Q(x) = x5 – 2x2 + 1– P(x).
PT
1
CM
4 tháng 7 2018
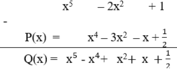
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x7 – 3x2 – x5 + x4 – x2 + 2x – 7
= x7 - (3x2+ x2) – x5+ x4 + 2x – 7
= x7 – 4x2 – x5+ x4 + 2x – 7
= x7 – x5 + x4 – 4x2 + 2x - 7
g(x) = x – 2x2 + x4 – x5 – x7 – 4x2 – 1
= x – ( 2x2 + 4x2) + x4 – x5 –x7 – 1
= x – 6x2 + x4 – x5 – x7 – 1
= -x7 – x5 + x4 – 6x2 + x – 1
* f(x) – g(x)
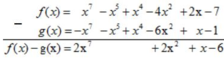
Vậy f(x) – g(x) = 2x7 + 2x2 + x - 6
20 tháng 3 2023
Thu gọn và sắp xếp phải k ạ?
`F(x)= (x^4-x^4)+(5x^2-8x^2)-4x+x^5+3+2x^3+2`
`F(x) = -3x^2-4x+x^5+3+2x^3+2`
`F(x)= x^5+2x^3-3x^2-4x+3+2`
H9
HT.Phong (9A5)
CTVHS
20 tháng 3 2023
\(F\left(x\right)=x^4+5x^2-4x+x^5-x^4-8x^2+3+2x^3+2\)
\(F\left(x\right)=x^5+\left(x^4-x^4\right)+2x^3+\left(5x^2-8x^2\right)-4x+\left(3+2\right)\)
\(F\left(x\right)=x^5+2x^3-3x^2-4x+5\)
23 tháng 8 2018
1) = \(\frac{3}{5}\)
2) =\(\frac{6}{7}\)
3)\(\frac{9}{13}\)
4)\(\frac{4}{13}\)