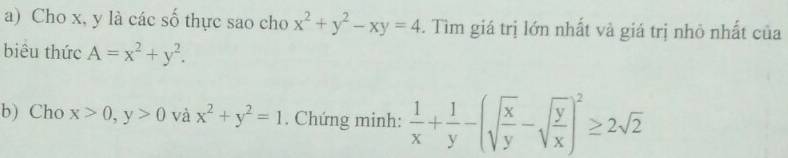ai cuu minh voi 💀💀💀
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MN
21 tháng 4 2021
I. Tình hình Việt Nam nửa cuối thế kỉ XIX
Vào những năm 60 của thế kỉ XIX:
- Thực dân Pháp ráo riết mở rộng cuộc chiến tranh xâm lược Nam Kì, chuẩn bị tấn công đánh chiếm cả nước ta.
- Triều đình Huế vẫn tiếp tục thực hiện chính sách nội trị, ngoại giao lỗi thời, lạc hậu.
=> Việt Nam rơi vào khủng hoảng nghiêm trọng. Cụ thể:
+ Chính trị: bộ máy chính quyền mục mát từ trung ương đến địa phương.
+ Kinh tế: nông nghiệp, thủ công nghiệp và thương nghiệp đình trệ, tài chính cạn kiệt.
+ Xã hội: đời sống nhân dân khốn khổ, mâu thuẫn dân tộc và mâu thuẫn giai cấp ngày càng gay gắt.
=> Tình hình trên làm cho các cuộc khởi nghĩa của nông dân lại tiếp tục bùng nổ dữ dội trong những năm cuối thế kỉ XIX.
=> CÁC TRÀO LƯU CẢI CÁCH DUY TÂN RA ĐỜI.
Lòng yêu nước của nhân dân ta thể hiện qua các cuộc khởi nghĩa nông dân và các cải cách duy tân...
7 tháng 6 2017
1. Số quả trứng con gà đó đẻ được trong 2 tuần là;
7x2=14 (quả trứng)
Đáp số; 14 quả trứng
2. 1 tuần=7 ngày
Bình đã về quê thăm ông bà ngoại số ngày là:
7+3=10 (ngày)
Đáp số: 10 ngày
3. Bình có số viên bi là:
5+4=9 (viên bi)
Đáp số: 9 viên bi
Căn có số viên bi là:
9+3=12 (viên bi)
Đáp số: 12 viên bi
LV
7 tháng 6 2017
1 : Số trứng con gà đó đẻ được trong 2 tuần là :
7 x 2 = 14 ( quả )
2 : 1 tuần 2 ngày = 9 ngày ; 1 tuần 3 ngày = 10 ngày
Bạn bình về thăm ông bà nội ngoại số ngày là :
9 + 10 = 19 ( ngày )
3 : Bình có số bi là :
5 + 4 = 9 ( viên )
Căn có số bi là :
9 + 3 = 12 ( viên )
24 tháng 3 2020
a) Gọi D là giao điểm của BM và AC
Gọi E là giao điểm của CM và AB
Do đó: CE⊥AB và BD⊥AC
Ta có: ΔEMB vuông tại E(CE⊥AB)
nên \(\widehat{EMB}+\widehat{EBM}=90^0\)(hai góc phụ nhau)(1)
Ta có: ΔDMC vuông tại D(BD⊥AC)
nên \(\widehat{DMC}+\widehat{DCM}=90^0\)(hai góc phụ nhau)(2)
mà \(\widehat{EMB}=\widehat{DMC}\)(hai góc đối đỉnh)(3)
nên \(\widehat{EBM}=\widehat{DCM}\)
hay \(\widehat{ABD}=\widehat{ACE}\)
Ta có: \(\widehat{ABD}+\widehat{CBD}=\widehat{ABC}\)(tia BD nằm giữa hai tia BA,BC)
\(\widehat{ACE}+\widehat{BCE}=\widehat{ACB}\)(tia CE nằm giữa hai tia CA,CB)
mà \(\widehat{ABC}=\widehat{ACD}\)(hai góc ở đáy của ΔABC cân tại A)
và \(\widehat{ABD}=\widehat{ACE}\)(cmt)
nên \(\widehat{DBC}=\widehat{ECB}\)
hay \(\widehat{MBC}=\widehat{MCB}\)
Xét ΔMBC có \(\widehat{MBC}=\widehat{MCB}\)(cmt)
nên ΔMBC cân tại M(định lí đảo của tam giác cân)
⇒MB=MC
Xét ΔEMB vuông tại E và ΔDMC vuông tại D có
MB=MC(cmt)
\(\widehat{EMB}=\widehat{DMC}\)(hai góc đối đỉnh)
Do đó: ΔEMB=ΔDMC(cạnh huyền-góc nhọn)
⇒EM=MD(hai cạnh tương ứng)
Xét ΔAEM vuông tại E và ΔADM vuông tại D có
AM là cạnh chung
EM=MD(cmt)
Do đó: ΔAEM=ΔADM(cạnh huyền-cạnh góc vuông)
⇒\(\widehat{EAM}=\widehat{DAM}\)(hai góc tương ứng)
hay \(\widehat{BAM}=\widehat{CAM}\)
mà tia AM nằm giữa hai tia AB, AC
nên AM là tia phân giác của \(\widehat{BAC}\)(đpcm)
b) Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: MB=MC(cmt)
nên M nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của BC
hay AM⊥BC(đpcm)
24 tháng 3 2020
a, - Gọi châm đường vuông góc kẻ từ B, C tới AC, AB lần lượt là H, K .
- Ta có : Tam giác ABC cân tại A .
=> AB = AC ( tính chất tam giác cân )
- Xét \(\Delta ABH\) và \(\Delta ACK\) có :
\(\left\{{}\begin{matrix}\widehat{BAC}\left(chung\right)\\AB=AC\left(cmt\right)\\\widehat{AHB}=\widehat{AKC}\left(=90^o\right)\end{matrix}\right.\)
=> \(\Delta ABH\) = \(\Delta ACK\) ( Ch - gn )
- Xét \(\Delta ABM\) và \(\Delta ACM\) có :
\(\left\{{}\begin{matrix}AB=AC\left(cmt\right)\\\widehat{ABM}=\widehat{ACM}\left(cmt\right)\\AM=AM\end{matrix}\right.\)
=> \(\Delta ABM\) = \(\Delta ACM\) ( c - g - c )
=> \(\widehat{A_1}=\widehat{A_2}\) ( góc tương ứng )
=> AM là tia phân giác của góc A . ( đpcm )
b, - Xét tam giác ABC cân tại A có :
+, AM là tia phân giác của góc A ( câu a )
=> AM là đường trung trực .
=> AM là đường cao .
=> AM vuông góc với BC ( đpcm )