 giải hộ mình bài 5 với ạaaa
giải hộ mình bài 5 với ạaaa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4.
a.
- Với \(m=0\Rightarrow y=-1\) hàm không có tiệm cận
- Với \(m\ne0\)
\(\lim\limits_{x\rightarrow\infty}\dfrac{x-1}{mx^2-x+1}=0\Rightarrow y=0\) là tiệm cận ngang
Xét phương trình \(mx^2-x+1=0\) có \(\Delta=1-4m\)
+ Với \(m>\dfrac{1}{4}\Rightarrow\Delta< 0\Rightarrow\) \(mx^2-x+1=0\) vô nghiệm hay ĐTHS ko có tiệm cận đứng
+ Với \(m=\dfrac{1}{4}\Rightarrow mx^2-x+1=0\) có nghiệm kép hay ĐTHS có 1 tiệm cận đứng
+ Với \(m< \dfrac{1}{4}\Rightarrow mx^2-x+1=0\) có 2 nghiệm pb (và luôn khác 1 với \(m\ne0\) ) nên ĐTHS có 2 tiệm cận đứng.
Kết luận...
4b.
- Với \(m=0\Rightarrow\lim\limits_{x\rightarrow\infty}\dfrac{-1}{x^2-x-2}=0\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow\left\{-1;2\right\}}\dfrac{-1}{x^2-x-2}=\infty\) nên \(x=-1;x=2\) là 2 tiệm cận đứng
- Với \(m\ne0\)
\(\lim\limits_{x\rightarrow\infty}\dfrac{mx^3-1}{x^2-x-2}=\infty\) nên ĐTHS không có tiệm cận ngang
Phương trình \(x^2-x-2=0\) có 2 nghiệm \(x=\left\{-1;2\right\}\) nên:
+ Nếu \(m=-1\Rightarrow-x^3-1=0\) có 1 nghiệm \(x=-1\Rightarrow\) hàm có đúng 1 tiệm cận đứng \(x=2\)
+ Nếu \(m=\dfrac{1}{8}\Rightarrow\dfrac{1}{8}x^3-1=0\) có 1 nghiệm \(x=2\Rightarrow\) ĐTHS hàm có đúng 1 tiệm cận đứng \(x=-1\)
+ Nếu \(m\ne\left\{-1;\dfrac{1}{8}\right\}\Rightarrow mx^3-1=0\) có nghiệm khác \(\left\{-1;2\right\}\Rightarrow\) ĐTHS có 2 tiệm cận đứng.
Kết luận...

Bài 5:
a: Ta có: \(x^2-8x+17\)
\(=x^2-8x+16+1\)
\(=\left(x-4\right)^2+1>0\forall x\)
b: Ta có: \(4x^2-12x+13\)
\(=4x^2-12x+9+4\)
\(=\left(2x-3\right)^2+4>0\forall x\)
c: Ta có: \(x^2-x+1\)
\(=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall x\)

cô bán hàng phải trả số tiền là :
90000-32000-25000-25000=8000[đồng]
đáp số :8000 đồng
cô bán hàng phải trả lại Bình số tiền là :
90000-32000-25000-25000=8000(đồng)
đáp số :8000 đồng
Đúng(0)

22,
1, Đặt √(3-√5) = A
=> √2A=√(6-2√5)
=> √2A=√(5-2√5+1)
=> √2A=|√5 -1|
=> A=\(\dfrac{\sqrt{5}-1}{\text{√2}}\)
=> A= \(\dfrac{\sqrt{10}-\sqrt{2}}{2}\)
2, Đặt √(7+3√5) = B
=> √2B=√(14+6√5)
=> √2B=√(9+2√45+5)
=> √2B=|3+√5|
=> B= \(\dfrac{3+\sqrt{5}}{\sqrt{2}}\)
=> B= \(\dfrac{3\sqrt{2}+\sqrt{10}}{2}\)
3,
Đặt √(9+√17) - √(9-√17) -\(\sqrt{2}\)=C
=> √2C=√(18+2√17) - √(18-2√17) -\(2\)
=> √2C=√(17+2√17+1) - √(17-2√17+1) -\(2\)
=> √2C=√17+1- √17+1 -\(2\)
=> √2C=0
=> C=0
26,
|3-2x|=2\(\sqrt{5}\)
TH1: 3-2x ≥ 0 ⇔ x≤\(\dfrac{-3}{2}\)
3-2x=2\(\sqrt{5}\)
-2x=2\(\sqrt{5}\) -3
x=\(\dfrac{3-2\sqrt{5}}{2}\) (KTMĐK)
TH2: 3-2x < 0 ⇔ x>\(\dfrac{-3}{2}\)
3-2x=-2\(\sqrt{5}\)
-2x=-2√5 -3
x=\(\dfrac{3+2\sqrt{5}}{2}\) (TMĐK)
Vậy x=\(\dfrac{3+2\sqrt{5}}{2}\)
2, \(\sqrt{x^2}\)=12 ⇔ |x|=12 ⇔ x=12, -12
3, \(\sqrt{x^2-2x+1}\)=7
⇔ |x-1|=7
TH1: x-1≥0 ⇔ x≥1
x-1=7 ⇔ x=8 (TMĐK)
TH2: x-1<0 ⇔ x<1
x-1=-7 ⇔ x=-6 (TMĐK)
Vậy x=8, -6
4, \(\sqrt{\left(x-1\right)^2}\)=x+3
⇔ |x-1|=x+3
TH1: x-1≥0 ⇔ x≥1
x-1=x+3 ⇔ 0x=4 (KTM)
TH2: x-1<0 ⇔ x<1
x-1=-x-3 ⇔ 2x=-2 ⇔x=-1 (TMĐK)
Vậy x=-1

Bài 5:
Chiều dài là (37+13):2=25(dm)
Chiều rộng là 37-25=12(dm)
Chiều cao là (25+12)/2=18,5(dm)
Diện tích xung quanh là:
\(74\cdot18.5=1369\left(dm^2\right)\)
Diện tích toàn phần là:
\(1369+2\cdot25\cdot12=1969\left(dm^2\right)\)

\(\left|1-2x\right|< 5-x\)
\(\Leftrightarrow-\left(5-x\right)< 1-2x< 5-x\)
\(\Leftrightarrow x-5< 1-2x< 5-x\)
\(\Leftrightarrow-4< x< 2\)




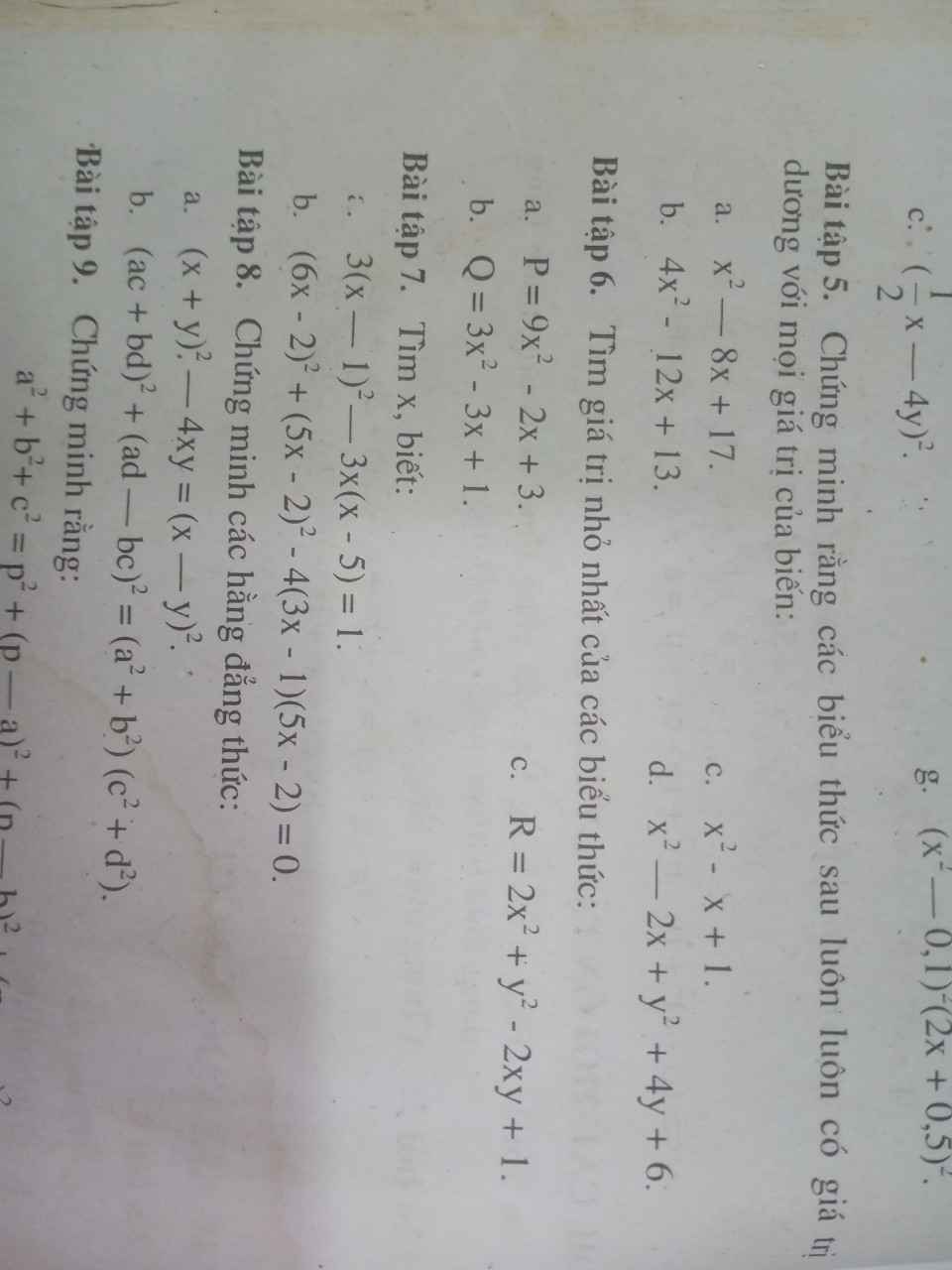

 giải bài 3 giúp Eem ạaaa
giải bài 3 giúp Eem ạaaa
Tý nx giúp cho
a) A = \(\dfrac{-3}{5}+\dfrac{1}{7}+\dfrac{-3}{5}\cdot\dfrac{6}{7}-1\dfrac{2}{5}\)
A= \(\dfrac{-3}{5}\cdot\left(\dfrac{1}{7}+\dfrac{6}{7}\right)-\dfrac{7}{5}\)
A = \(\dfrac{-3}{5}-\dfrac{7}{5}\)
A \(=-2\)
Số đối của -2 là 2
b) \(B=\dfrac{-5}{12}-\dfrac{1}{18}+\dfrac{7}{12}+\dfrac{1}{2}\)
\(B=\dfrac{-15}{36}-\dfrac{2}{36}+\dfrac{21}{36}+\dfrac{18}{36}\)
\(B=-\dfrac{17}{36}+\dfrac{39}{36}\)
B = \(\dfrac{22}{36}=\dfrac{11}{18}\)
số đối của \(\dfrac{11}{18}\) là \(-\dfrac{11}{18}\)
c) C = \(\dfrac{-7}{19}\cdot\dfrac{13}{14}-\dfrac{7}{19}\cdot\dfrac{1}{14}\)
C = \(\dfrac{7}{19}\cdot\dfrac{-13}{14}-\dfrac{7}{19}\cdot\dfrac{1}{14}\)
C = \(\dfrac{7}{19}\cdot\left(\dfrac{-13}{14}-\dfrac{1}{14}\right)\)
\(C=\dfrac{7}{19}\cdot\left(-1\right)\)
C = \(\dfrac{-7}{19}\)
số đối của \(\dfrac{-7}{19}\) là \(\dfrac{7}{19}\)