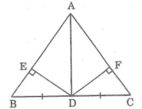
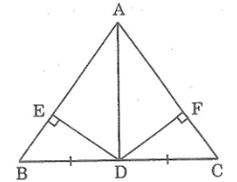
Bài 1Cho tam giác ABC cân tại A, D là trung điểm của BC, E và F là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh DE=DF.
Bài 2 tam giác ABC, E là trung điểm của AC. Qua E kẻ đường thẳng || BC cắt AB ở F. Đường thẳng qua E cắt BC tại D. Chứng minh F là trung điểm của AB và D là trung điểm của BC.
Ai giúp e giải 2 bài này với