có thể tìm được 2 số TN ava2 b để thỏa mãn :
33a + 22b = 110115
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



33a+22b=110115
TH1:
33a=110115
a=110115:33
a=36705/11
=>22b=110115-(33.36705/11)
=>22b=0
b=0:22
=>b=0
TH2
33a+22b=110115
22b=110115
b=110115:22
b=110115/22
=>33a=110115-(22.110115/22)
33a=0
a=0:33
=> a=0

Ta có: 33.a+22.b=110115
=> 3a+2b=10010,45454545455
VÌ 33 và 22 đều chia hết cho 11 => 33.a+22.b đều chia hết cho 11
Tuy nhiên 110115 không chia hết cho 11 ( Vô lý)
=> a,b không tồn tại để 33.a+22.b= 110115
33a + 22b = 11(3a+2b) chia hết cho 11 mà 110115 không chia hết cho 11 nên không tồn tại hai số tự nhiên a và b nào thỏa mãn đề bài.

x = -2 là nghiệm của phương trình: a x 2 + bx + c = 0, ta có:
4a - 2b + c = 0
x = 3 là nghiệm của phương trình: a x 2 + bx + c = 0 ta có:
9a + 3b + c = 0
Ba số a, b, c là nghiệm của hệ phương trình:
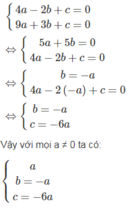
thì phương trình a x 2 + bx + c = 0 có nghiệm x 1 = -2; x 2 = 3
Ví dụ: a = 2, b = -2, c = -12 ta có phương trình:
2 x 2 - 2x - 12 = 0
⇒ x 2 - x - 6 = 0
⇒ (x + 2)(x - 3) = 0
Có nghiệm: x 1 = - 2; x 2 = 3
Có vô số bộ ba a, b, c thỏa mãn yêu cầu bài toán.

c có ba kết quả là nhỏ nhất, lớn nhất và lớn hơn a nhưng nhỏ hơn b
- nhỏ nhất ta có dạng: c<a<b<5\(\Rightarrow\)c = 0,1,2
- lớn nhất ta có dạng: a<b<c\(\ge\)5\(\Rightarrow\)c = 5 vì b<5
- lớn hơn a nhưng nhỏ hơn b ta có dạng: a<c<b<5 \(\Rightarrow\)nếu b = 4 thì c = 3; nếu b = 3 thì c = 2; nếu b = 2 thì c = 1 và a = 0\(\Rightarrow\)c = 3,2,1
Hk tốt

a, có \(22⋮11;77⋮11;99⋮11\Rightarrow22+77+99⋮11\).
b, có \(88⋮11;30\)không chia hết cho 11;\(66⋮11\Rightarrow88+30+66\)không chia hết cho 11.
c, có \(11⋮11;22⋮22\Rightarrow11a+22b⋮11\).
d, có \(33⋮11;17\)không chia hết cho 11 \(\Rightarrow33a+17\)không chia hết cho 11.
a,vì 22 chia hết cho 11
77 chia hết cho 11
99 chia hết cho 11
=>22+77+99 chia hết cho 11
b,vì 88 chia hết cho 11
30 không chia hết cho 11
66 chia hết cho 11
=>88+30+66 ko chia hết cho 11
c,vì 11a chia hết cho 11(do 11 chia hết cho 11)
22b chia hết cho 11(do 22 chia hết cho 11)
=>11a+22b chia hết cho 11
d,vì 33a chia hết cho 11(do 33 chia hết cho 11)
17 ko chia hết cho 11
=>33a+17 ko chia hết cho11
