Bài 3 (1 điểm) : Chứng minh rằng nếu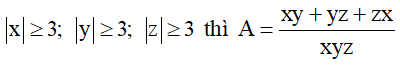 
có giá trị nhỏ hơn hoặc bằng 1.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
GH
0
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 3 2019
\(\left\{{}\begin{matrix}\left|x\right|\ge3\\\left|y\right|\ge3\\\left|z\right|\ge3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left|\dfrac{1}{x}\right|\le\dfrac{1}{3}\\\left|\dfrac{1}{y}\right|\le\dfrac{1}{3}\\\left|\dfrac{1}{z}\right|\le\dfrac{1}{3}\end{matrix}\right.\)
\(\left|A\right|=\left|\dfrac{xy+yz+xz}{xyz}\right|=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\le\left|\dfrac{1}{x}\right|+\left|\dfrac{1}{y}\right|+\left|\dfrac{1}{z}\right|\le\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}=1\)
\(\Rightarrow A\le\left|A\right|\le1\) (đpcm)
Dấu "=" xảy ra khi \(x=y=z=3\)
6 tháng 8 2016
2)81^10-27^13-9^21=3^40-3^39-3^42=3^39(3-1-3^3) =3^39.(-25)=3^37.9.(-25)=3^37.(-225) chia hết cho 225
28 tháng 8 2015
a2+b2+c2=ab+ac+bc
<=>2a2+2b2+2c2=2ab+2ac+2bc
<=>a2-2ab+b2+a2-2ac+c2+b2-2bc=0
<=>(a-b)2+(a-c)2+(b-c)2=0
<=>a-b=0 và a-c=0 và b-c=0
<=>a=b=c
20 tháng 4 2018
1)
Ta có : \(5-2x< 3+x\)
\(\Leftrightarrow-2x-x< 3-5\)
\(\Leftrightarrow-3x< -2\)
\(\Leftrightarrow x>\frac{2}{3}\)
Vậy bất phương trình có tập nghiệm \(\left\{x/x>\frac{2}{3}\right\}\)
20 tháng 4 2018
2)
Ta có : \(a^2+b^2+2-2\left(a+b\right)\)
\(=a^2+b^2+2-2a-2b\)
\(=\left(a^2-2a+1\right)+\left(b^2-2b+1\right)\)
\(=\left(a-1\right)^2+\left(b-1\right)^2\)
Mà : \(\left(a-1\right)^2\ge0\forall a\)
\(\left(b-1\right)^2\ge0\forall b\)
\(\Rightarrow\left(a-1\right)^2+\left(b-1\right)^2\ge0\forall a;b\) ( luôn đúng )
\(\Rightarrow a^2+b^2+2\ge2\left(a+b\right)\left(đpcm\right)\)
Vậy \(a^2+b^2+2\ge2\left(a+b\right)\)