giải phương trình (x-5)(x-1)=(2x+1)(\(\dfrac{1}{2}\)x-3)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 2 2021
`(3x-1)/(x-1)-(2x+5)/(x+3)+4/(x^2+2x-3)=1(x ne 1,-3)`
`<=>((3x-1)(x+3))/(x^2+2x-3)-((2x+5)(x-1))/(x^2+2x-3)+4/(x^2+2x-3)=(x^2+2x-3)/(x^2+2x-3)`
`<=>(3x-1)(x+3)-(2x+5)(x-1)+4=x^2+2x-3`
`<=>3x^2+8x-3-2x^2-3x+5+4=x^2+2x-3`
`<=>x^2+5x+6=x^2+2x-3`
`<=>3x=-9`
`<=>x=-3(loại)`
Vậy `S={cancel0}`
27 tháng 2 2021
ĐKXĐ: \(x\notin\left\{1;-3\right\}\)
Ta có: \(\dfrac{3x-1}{x-1}-\dfrac{2x+5}{x+3}+\dfrac{4}{x^2+2x-3}=1\)
\(\Leftrightarrow\dfrac{\left(3x-1\right)\left(x+3\right)}{\left(x-1\right)\left(x+3\right)}-\dfrac{\left(2x+5\right)\left(x-1\right)}{\left(x+3\right)\left(x-1\right)}+\dfrac{4}{\left(x+3\right)\left(x-1\right)}=\dfrac{x^2+2x-3}{\left(x+3\right)\left(x-1\right)}\)
\(\Leftrightarrow\dfrac{3x^2+9x-x-3-\left(2x^2-2x+5x-5\right)+4}{\left(x+3\right)\left(x-1\right)}=\dfrac{x^2+2x-3}{\left(x+3\right)\left(x-1\right)}\)
\(\Leftrightarrow\dfrac{3x^2+8x-3-\left(2x^2+3x-5\right)+4}{\left(x+3\right)\left(x-1\right)}=\dfrac{x^2+2x-3}{\left(x+3\right)\left(x-1\right)}\)
\(\Leftrightarrow\dfrac{3x^2+8x+1-2x^2-3x+5}{\left(x+3\right)\left(x-1\right)}=\dfrac{x^2+2x-3}{\left(x+3\right)\left(x-1\right)}\)
Suy ra: \(x^2+5x+6-x^2-2x+3=0\)
\(\Leftrightarrow3x+9=0\)
\(\Leftrightarrow3x=-9\)
hay x=-3(Không nhận)
Vậy: \(S=\varnothing\)
HP
16 tháng 3 2021
1.
ĐK: \(x\ne7;x\ne-1;x\ne3\)
\(\dfrac{2x-5}{x^2-6x-7}\le\dfrac{1}{x-3}\left(1\right)\)
TH1: \(x< -1\)
\(\left(1\right)\Leftrightarrow\left(2x-5\right)\left(x-3\right)\ge x^2-6x-7\)
\(\Leftrightarrow2x^2-11x+15\ge x^2-6x-7\)
\(\Leftrightarrow x^2-5x+22\ge0\)
\(\Leftrightarrow\) Bất phương trình đúng với mọi \(x< -1\)
TH2: \(-1< x< 3\)
\(\left(1\right)\Leftrightarrow\left(3-x\right)\left(2x-5\right)\ge\left(7-x\right)\left(x+1\right)\)
\(\Leftrightarrow-2x^2+11x-15\ge-x^2+6x+7\)
\(\Leftrightarrow-x^2+5x-22\ge0\)
\(\Rightarrow\) vô nghiệm
TH3: \(3< x< 7\)
Khi đó \(\dfrac{2x-5}{x^2-6x-7}\le0\); \(\dfrac{1}{x-3}>0\)
\(\Rightarrow\) Bất phương trình đúng với mọi \(3< x< 7\)
TH4: \(x>7\)
\(\left(1\right)\Leftrightarrow\left(2x-5\right)\left(x-3\right)\le x^2-6x-7\)
\(\Leftrightarrow2x^2-11x+15\le x^2-6x-7\)
\(\Leftrightarrow x^2-5x+22\le0\)
\(\Rightarrow\) vô nghiệm
Vậy ...
Các bài kia tương tự, chứ giải ra mệt lắm.
BC
2
25 tháng 2 2021
`1+(x-2)/(1-x)+(2x^2-5)/(x^3-1)=4/(x^2+x+1)(x ne 1)`
`<=>(x^3-1)/(x^3-1)-((x-2)(x^2+x+1))/(x^3-1)+(2x^2-5)/(x^3-1)=(4(x-1))/(x^3-1)`
`<=>x^3-1-(x-2)(x^2+x+1)+2x^2-5=4(x-1)`
`<=>x^3-1-(x^3-x^2-x-2)+2x^2-5=4x-4`
`<=>x^3-1-x^3+x^2+x+2+2x^2-5-4x+4=0`
`<=>3x^2-3x+2=0`
`<=>x^2-2/3 x+2/3=0`
`<=>x^2-2.x. 1/3+1/9+5/9=0`
`<=>(x-1/3)^2=-5/9` vô lý
Vậy phương trình vô nghiệm.
25 tháng 2 2021
ĐKXĐ: \(x\ne1\)
Ta có: \(1+\dfrac{x-2}{1-x}+\dfrac{2x^2-5}{x^3-1}=\dfrac{4}{x^2+x+1}\)
\(\Leftrightarrow\dfrac{x^3-1}{\left(x-1\right)\left(x^2+x+1\right)}-\dfrac{\left(x-2\right)\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}+\dfrac{2x^2-5}{\left(x-1\right)\left(x^2+x+1\right)}=\dfrac{4\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
Suy ra: \(x^3-1-\left(x^3+x^2+x-2x^2-2x-2\right)+2x^2-5=4x-4\)
\(\Leftrightarrow x^3-1-x^3+x^2+x+2+2x^2-5-4x+4=0\)
\(\Leftrightarrow3x^2-3x=0\)
\(\Leftrightarrow3x\left(x-1\right)=0\)
mà 3>0
nên x(x-1)=0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(nhận\right)\\x=1\left(loại\right)\end{matrix}\right.\)
Vậy: S={0}
28 tháng 8 2021
a: Ta có: \(6-4x=5(x+3)+3\)
\(\Leftrightarrow6-4x-5x-12-3=0\)
\(\Leftrightarrow-9x=9\)
hay x=-1
b: Ta có: \(\dfrac{x+3}{2}-1=\dfrac{x-1}{3}+\dfrac{x+5}{6}\)
\(\Leftrightarrow15x+45-30=10x-30+5x+25\)
\(\Leftrightarrow15=-5\left(loại\right)\)
c: Ta có: \(\left(x-2\right)\left(2x+1\right)-3\left(x-2\right)=0\)
\(\Leftrightarrow2\left(x-2\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=1\end{matrix}\right.\)
29 tháng 8 2021
d: Ta có: \(\dfrac{2}{x^2-2x}+\dfrac{1}{x}=\dfrac{x+2}{x-2}\)
\(\Leftrightarrow2+x-2=x^2+2x\)
\(\Leftrightarrow x^2+x=0\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(loại\right)\\x=-1\left(nhận\right)\end{matrix}\right.\)
19 tháng 8 2021
1: Ta có: \(\dfrac{3}{x+2}-\dfrac{x-1}{x^2-4}=\dfrac{2}{x-2}\)
Suy ra: \(3x-6-x+1=2x+4\)
\(\Leftrightarrow2x-5=2x+4\left(vôlý\right)\)
2: Ta có: \(\dfrac{x-5}{2x-3}-\dfrac{x}{2x+3}=\dfrac{1-6x}{4x^2-9}\)
Suy ra: \(\left(x-5\right)\left(2x+3\right)-x\left(2x-3\right)=1-6x\)
\(\Leftrightarrow2x^2-7x-15-2x^2+6x+6x-1=0\)
\(\Leftrightarrow5x=16\)
hay \(x=\dfrac{16}{5}\)
31 tháng 7 2023
a: =>(x-2)(2x+5)=0
=>x-2=0 hoặc 2x+5=0
=>x=2 hoặc x=-5/2
c: \(\dfrac{2x}{x-1}-\dfrac{x}{x+1}=1\)
=>\(\dfrac{2x^2+2x-x^2+x}{x^2-1}=1\)
=>x^2+3x=x^2-1
=>3x=-1
=>x=-1/3
22 tháng 3 2022
\(a,\Leftrightarrow\left(x-2\right)\left(2x+5\right)=0\\ \Leftrightarrow\left\{{}\begin{matrix}x-2=0\\2x+5=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}x=2\\x=\dfrac{5}{2}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm S = \(\left\{2;\dfrac{5}{2}\right\}\)
\(c,\Leftrightarrow2x.\left(x+1\right)-x.\left(x-1\right)=\left(x-1\right)\left(x+1\right)\) ( ĐKXĐ: \(x\ne-1;x\ne1\) )
\(\Leftrightarrow2x^2+2x-x^2+x=x^2-1\\ \Leftrightarrow x^2-x^2+3x=-1\\ \Leftrightarrow3x=-1\\ \Leftrightarrow x=-\dfrac{1}{3}\) ( nhận )
Vậy phương trình có tập nghiệm S = \(\left\{-\dfrac{1}{3}\right\}\)
MS
2
TQ
28 tháng 1 2022
1) \(ĐK:x\ne2\)
Nếu \(x>2\)
BPT ⇔ \(x^2-2x+5-\left(x-1\right)\left(x-2\right)\ge0\) ⇔ \(x^2-2x+5-\left(x^2-3x+3\right)\ge0\)
⇔\(x+2\ge0\) ⇔\(x\ge-2\) ⇒ Lấy \(x\ge2\)
Nếu \(x< 2\)
BPT ⇔\(\dfrac{-\left(x^2-2x+5\right)}{x-2}-x+1\ge0\) ⇔\(-x^2+2x-5-\left(x-1\right)\left(x-2\right)\ge0\)
⇔\(-x^2+2x-5-x^2+3x-2\ge0\)
⇔\(-2x^2+5x-7\ge0\)
⇔\(x^2-\dfrac{5}{2}x+\dfrac{7}{2}\le0\)
⇔\(\left(x-\dfrac{5}{4}\right)^2\le\dfrac{11}{4}\)
⇔\(\left[{}\begin{matrix}x-\dfrac{5}{4}\le\dfrac{11}{4}\\x-\dfrac{5}{4}\le\dfrac{-11}{4}\end{matrix}\right.\) ⇔\(\left[{}\begin{matrix}x\le4\\x\le\dfrac{-3}{2}\end{matrix}\right.\) ⇔ \(x\le\dfrac{-3}{2}\)
S= [2;+∞)U(-∞;\(\dfrac{-3}{2}\)]
TQ
28 tháng 1 2022
2) \(ĐK:x\ne-1\)
Nếu \(x>-1\)
BPT ⇔ \(2x-3-2\left(x+1\right)< 0\) ⇔\(2x-3-2x-2< 0\)
⇔\(-5< 0\) ( luôn đúng với mọi \(x>-1\))
Nếu \(x< -1\)
BPT⇔\(\dfrac{-\left(2x-3\right)}{x+1}-2< 0\) ⇔\(-\left(2x-3\right)-2\left(x+1\right)< 0\) ⇔\(-4x+1< 0\) ⇔ \(x>\dfrac{-1}{4}\)
Vậy S=....
28 tháng 1 2022
\(\dfrac{2x-1}{x+1}-2< 0.\left(x\ne-1\right).\\ \Leftrightarrow\dfrac{2x-1-2x-2}{x+1}< 0.\Leftrightarrow\dfrac{-3}{x+1}< 0.\)
Mà \(-3< 0.\)
\(\Rightarrow x+1>0.\Leftrightarrow x>-1\left(TMĐK\right).\)
\(\dfrac{x^2-2x+5}{x-2}-x+1\ge0.\left(x\ne2\right).\\ \Leftrightarrow\dfrac{x^2-2x+5-x^2+2x+x-2}{x-2}\ge0.\\ \Leftrightarrow\dfrac{x+3}{x-2}\ge0.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+3\ge0.\\x-2\ge0.\end{matrix}\right.\\\left\{{}\begin{matrix}x+3\le0.\\x-2\le0.\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge-3.\\x\ge2.\end{matrix}\right.\\\left\{{}\begin{matrix}x\le-3.\\x\le2.\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge2.\\x\le-3.\end{matrix}\right.\)
Kết hợp ĐKXĐ.
\(\Rightarrow\left[{}\begin{matrix}x>2.\\x\le-3.\end{matrix}\right.\)
\(\dfrac{\left(1+2x\right)\left(x-2\right)}{\left(2x+3\right)\left(1-x\right)}\le0.\left(x\ne1;x\ne\dfrac{-3}{2}\right).\)
Đặt \(\dfrac{\left(1+2x\right)\left(x-2\right)}{\left(2x+3\right)\left(1-x\right)}=f\left(x\right).\)
Ta có bảng sau:
| \(x\) | \(-\infty\) \(-\dfrac{3}{2}\) \(-\dfrac{1}{2}\) \(1\) \(2\) \(+\infty\) |
| \(1+2x\) | - | - 0 + | + | + |
| \(x-2\) | - | - | - | - 0 + |
| \(2x+3\) | - 0 + | + | + | + |
| \(1-x\) | + | + | + 0 - | - |
| \(f\left(x\right)\) | - || + 0 - || + 0 - |
Vậy \(f\left(x\right)\ge0.\Leftrightarrow x\in\left(\dfrac{-3}{2};\dfrac{-1}{2}\right)\cup\)(1;2].
28 tháng 1 2022
\(1,\) thiếu đề
\(2,\dfrac{5x+2}{6}-\dfrac{8x-1}{3}=\dfrac{4x+2}{5}-5\)
\(\Leftrightarrow\dfrac{5\left(5x+2\right)}{30}-\dfrac{10\left(8x-1\right)}{30}=\dfrac{6\left(4x+2\right)}{30}-\dfrac{150}{30}\)
\(\Leftrightarrow5\left(5x+2\right)-10\left(8x-1\right)=6\left(4x+2\right)-150\)
\(\Leftrightarrow25x+10-80x+10=24x+12-150\)
\(\Leftrightarrow-55x+20=24x-138\)
\(\Leftrightarrow24x-138+55x-20=0\)
\(\Leftrightarrow79x-158=0\)
\(\Leftrightarrow x=2\)
\(3,ĐKXĐ:\left\{{}\begin{matrix}x\ne1\\x\ne-1\\x\ne3\end{matrix}\right.\\ \dfrac{x}{2x-6}+\dfrac{x}{2x-2}=\dfrac{-2x}{\left(x+1\right)\left(3-x\right)}\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}+\dfrac{2x}{\left(x+1\right)\left(3-x\right)}=0\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}+\dfrac{x}{2\left(x-1\right)}-\dfrac{2x}{\left(x+1\right)\left(x-3\right)}=0\)
\(\Leftrightarrow x\left(\dfrac{1}{2\left(x-3\right)}+\dfrac{1}{2\left(x-1\right)}-\dfrac{2}{\left(x+1\right)\left(x-3\right)}\right)=0\)
\(\Leftrightarrow x\left(\dfrac{\left(x-1\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{\left(x-3\right)\left(x+1\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4\left(x-1\right)}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)
\(\Leftrightarrow x\left(\dfrac{x^2-1}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}+\dfrac{x^2-2x-3}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}-\dfrac{4x-4}{2\left(x+1\right)\left(x-3\right)\left(x-1\right)}\right)=0\)
\(\Leftrightarrow x.\dfrac{x^2-1+x^2-2x-3-4x+4}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x.\dfrac{2x^2-6x}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x.\dfrac{2x\left(x-3\right)}{2\left(x-1\right)\left(x-3\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x.\dfrac{x}{\left(x-1\right)\left(x+1\right)}=0\)
\(\Leftrightarrow\dfrac{x^2}{\left(x-1\right)\left(x+1\right)}=0\)
\(\Leftrightarrow x=0\)
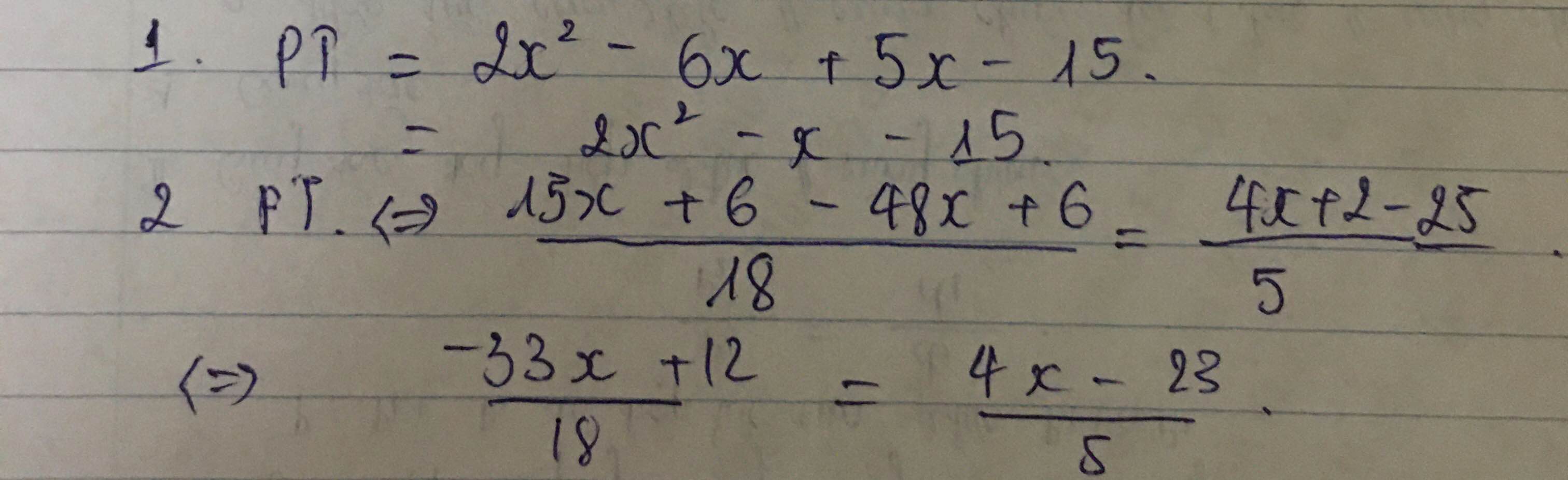
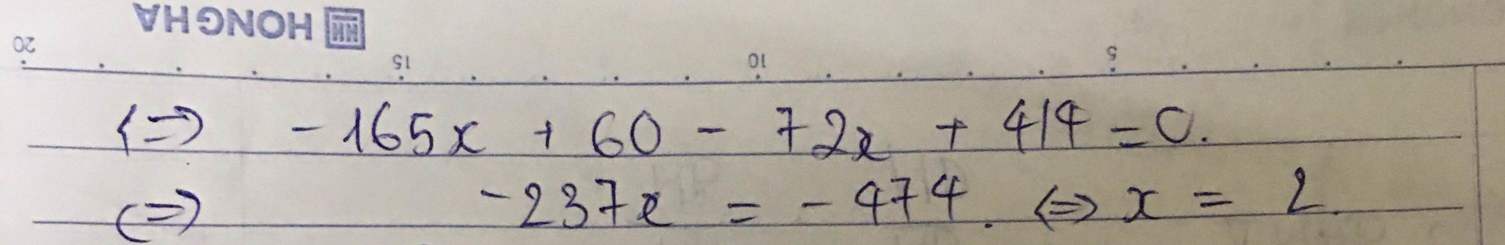
\(\left(x-5\right)\left(x-1\right)=\left(2x+1\right)\left(\dfrac{1}{2}x-3\right)\\ \Leftrightarrow x^2-6x+5=x^2-\dfrac{11}{2}x-3\\ \Leftrightarrow x^2-6x+5-x^2+\dfrac{11}{2}x+3=0\\ \Leftrightarrow-\dfrac{1}{2}x+8=0\\ \Leftrightarrow x=16\)