Một con lắc lò xo nằm ngang gồm vật nặng khối lượng m và lò xo có độ cứng K. Từ vị trí cân bằng O, đưa vật ra đến vị trí lò xo giãn 12cm rồi thả nhẹ, bỏ qua mọi ma sát lực cản. Tại chỗ có động năng bằng thế năng vật cách vị trí cân bằng O là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
1 tháng 11 2018
Chọn đáp án B
Động năng cực đại là cơ năng của con lắc: E = 1 2 k A 2 = 1 2 .100. 4.10 − 2 2 = 0 , 08
VT
27 tháng 1 2018
Đáp án D
+ Tại thời điểm ban đầu ta có 
+ Đưa vật tới vị trí lò xo giãn 20 cm thì có thêm vật 
gắn vào
m
1
nên khi đó ta sẽ có VTCB mới O’ dịch xuống dưới so với O 1 đoạn bằng:
.
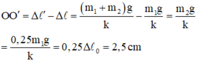+ Tại vị trí đó người ta thả nhẹ cho hệ chuyển động nên: 
+ Khi về đến O thì m 2 tuột khỏi m 1 khi đó hệ chỉ còn lại m 1 dao động với VTCB O, gọi biên độ khi đó là A 1 .
+ Vận tốc tại điểm O tính theo biên độ A’ bằng vận tốc cực đại của vật khi có biên độ là A 1
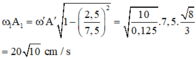
+ Biên độ dao động của m 1 sau khi m 2 tuột là:
VT
26 tháng 7 2018
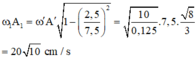
Đáp án D
+ Tại thời điểm ban đầu ta có ∆ l 0 = 10 c m
+ Đưa vật tới vị trí lò xo giãn 20 cm thì có thêm vật m2 = 0,25m1 gắn vào m1 nên khi đó ta sẽ vó VTCB mới O’ dịch xuống dưới so với O 1 đoạn bằng:
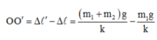
+ Khi về đến O thì m2 tuột khỏi m1 khi đó hệ chỉ còn lại m1 dao động với VTCB O, gọi biên độ khi đó là A1.
+ Vận tốc tại điểm O tính theo biên độ A’ bằng vận tốc cực đại của vật khi có biên độ là A1
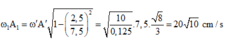
+ Biên độ dao động của m1 sau khi m2 tuột là: A 1 = 20 10 10 0 . 1 = 2 10 ≈ 6 , 32 c m
9 tháng 3 2022
a)Thế năng đàn hồi:
\(W_{đh}=\dfrac{1}{2}k\left(\Delta x\right)^2=\dfrac{1}{2}\cdot200\cdot0,04^2=0,16J\)
b)Cơ năng tại vị trí cân bằng của quả cầu:
\(W=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot0,1\cdot v^2\)
Bảo toàn cơ năng: \(W_{đh}=W\)
\(\Rightarrow0,16=\dfrac{1}{2}\cdot0,1\cdot v^2\Rightarrow v=\dfrac{4\sqrt{5}}{5}\)m/s
VT
15 tháng 1 2017
Chu kì của dao động T = 2 π m k = 2 π 0 , 2 10 = 0 , 89 s
+ Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 1.0 , 2.10 10 = 2 c m
→ Biên độ dao động của vật trong nửa chu kì đầu tiên là A 1 = X 0 – x 0 = 6 – 2 = 4 c m .
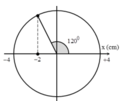
+ Lực đàn hồi của lò xo là nhỏ nhất khi vật đi qua vị trí lò xo không biến dạng, trong nửa chu kì đầu tiên đối vị trí cân bằng tạm O 1 thì vị trí lò xo không biến dạng có li độ x = –2 cm.
→ Thời gian tương ứng Δ t = 120 0 360 0 T = 0 , 296 s
Đáp án A
6 tháng 3 2022
Câu 19.
a)Thế năng đàn hồi:
\(W_{đh}=\dfrac{1}{2}k\cdot\left(\Delta x\right)^2=\dfrac{1}{2}\cdot100\cdot0,05^2=0,125J\)
b)Cơ năng vật tại vị trí cân bằng:
\(W'=\dfrac{1}{2}mv^2+\dfrac{1}{2}k\cdot\left(\Delta x\right)^2=\dfrac{1}{2}\cdot0,2\cdot v^2+\dfrac{1}{2}\cdot100\cdot0^2\)
\(=0,1v^2\left(J\right)\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow0,125=\dfrac{1}{2}mv^2\Rightarrow v=\dfrac{\sqrt{5}}{2}\)m/s
6 tháng 3 2022
Câu 20.
a)Động năng: \(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}\cdot0,1\cdot5^2=1,25J\)
Thế năng: \(W_t=mgz=0,1\cdot10\cdot10=10J\)
Cơ năng: \(W=W_đ+W_t=1,25+10=11,25J\)
b)Cơ năng tại nơi có độ cao cực đại: \(W_1=mgh_{max}\left(J\right)\)
Bảo toàn cơ năng: \(W=W_1\)
\(\Rightarrow11,25=mgh_{max}\Rightarrow h_{max}=\dfrac{11,25}{0,1\cdot10}=11,25m\)
c)Lực cản: \(F_c=0,2P=0,2\cdot10\cdot0,1=0,2N\)
Cơ năng tại nơi đây:
\(W_2=\left(mg+F_c\right)\cdot h'_{max}=\left(0,1\cdot10+0,2\right)\cdot h'_{max}\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow0,125=\left(0,1\cdot10+0,2\right)\cdot h'_{max}\)
\(\Rightarrow h'_{max}=0,1m\)
VT
20 tháng 10 2019
Đáp án B
Fdhmax = k(∆l + A) → Fdhmax = mω2(∆l + ∆l)
↔ Fdhmax =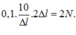 
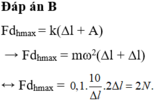
Thế năng đàn hồi:
\(W_{đh}=\dfrac{1}{2}k\cdot\left(\Delta x\right)^2=\dfrac{1}{2}\cdot k\cdot0,12^2=7,2\cdot10^{-3}k\left(J\right)\)
Cơ năng tại vị trí cân bằng của quả cầu:
\(W=\dfrac{1}{2}mv^2+mgz\left(J\right)\)
Bảo toàn cơ năng: \(W_{đh}=W\)
\(\Rightarrow7,2\cdot10^{-3}k=\dfrac{1}{2}mv^2+mgz\)
\(\Rightarrow0,0144k=mv^2+2mgz\)
\(\Rightarrow z=\dfrac{0,0144k-mv^2}{2mg}\)
Nếu có số liệu cụ thể thì bạn tự thay vào nha