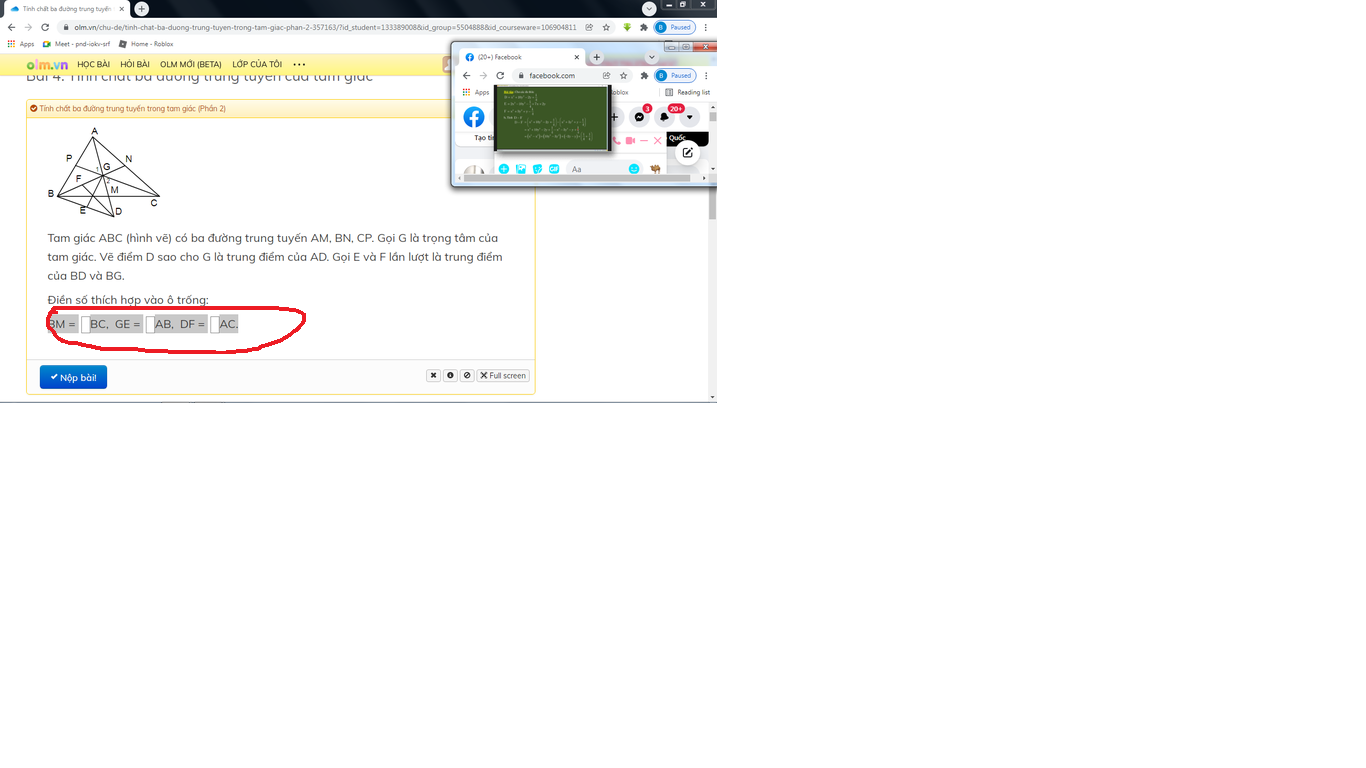
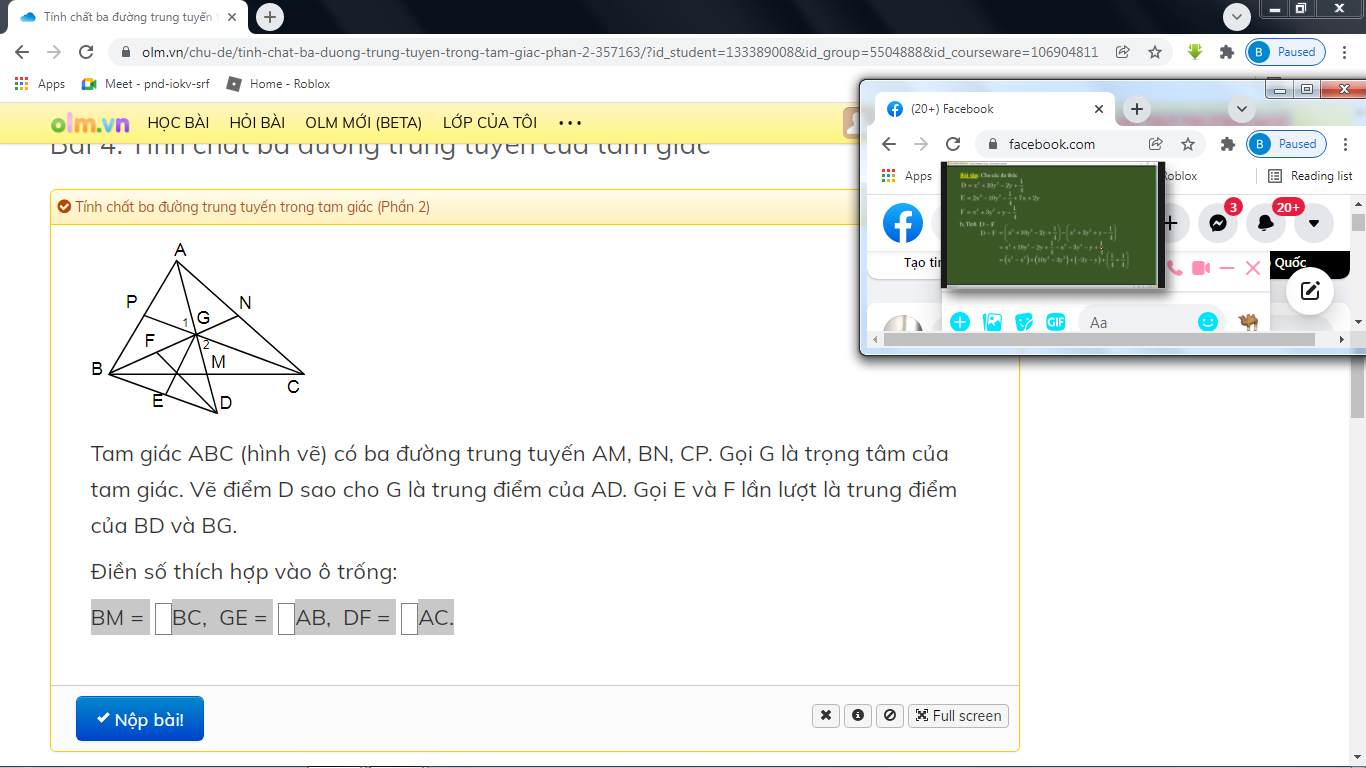
Tam giác ABC (hình vẽ) có ba đường trung tuyến AM, BN, CP. Gọi G là trọng tâm của tam giác. Vẽ điểm D sao cho G là trung điểm của AD. Gọi E và F lần lượt là trung điểm của BD và BG.
Điền số thích hợp vào ô trống:
BM =....BC, GE =....AB, DF =....AC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Do G là trọng tâm tam giác ABC nên AG = 2GM. Lại có AG = GD nên GD = 2GM hay GM = DM.
Xét tam giác DMB và tam giác GMC có:
DM = GM
BM = CM
\(\widehat{DMB}=\widehat{GMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta DMB=\Delta GMC\left(c-g-c\right)\)
\(\Rightarrow BD=CG\)
b) Do \(\Delta DMB=\Delta GMC\Rightarrow\widehat{FBM}=\widehat{ECM}\)
Xét tam giác FBM và tam giác ECM có:
\(\widehat{FMB}=\widehat{EMC}=90^o\)
BM = CM
\(\widehat{FBM}=\widehat{ECM}\)
\(\Rightarrow\Delta FBM=\Delta ECM\) (Cạnh góc vuông - góc nhọn kề)
\(\Rightarrow BF=CE\left(đpcm\right)\)

a/
Ta có
MB=MC (gt); MG=MI (gt) => BICG là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành)
Ta có
\(GN=\dfrac{BG}{2}\) (tính chất trọng tâm tg)
Mà \(BE=GE=\dfrac{BG}{2}\) (gt)
=> GN=GE
Cứng minh tương tự ta cũng có GM=GF
=> MNFE là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành)
b/
Khi MNFE là HCN \(\Rightarrow EF\perp FN\) (1)
Xét tg AGC có
FA=FG; NA=NC => FN là đường trung bình của tg AGC
=> FN//CG (2)
Từ (1) và (2) \(\Rightarrow CG\perp EF\) (3)
Xét tg ABG có
EB=EG; FA=FG => EF là đường trung bình của tg ABG => EF//AB (4)
Từ (3) và (4) \(\Rightarrow CG\perp AB\) => CG là đường cao của tg ABC
Mà CG cũng là trung tuyến của tg ABC (trong tg 3 đường trung tuyến đồng quy)
=> tg ABC cân tại C (Tam giác có đường cao đồng thời là đường trung tuyến là tg cân)
c/
Khi BICG là hình thoi
\(\Rightarrow GI\perp BC\) (trong hình thoi hai đường chéo vuông góc với nhau)
\(\Rightarrow AM\perp BC\) => AM là đường cao của tg ABC
Mà AM cũng là trung tuyến của tg ABC
=> tg ABC cân tại A (trong tg đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)

suy ra: MG=1/2AM,suy ra: MG=1/2AG
mà AG=GD suy ra: MG=1/2GD -> MG=MD( điều phải cm)
2. xét tam giác BDM và tam giác CGM
góc GMC=góc DMB (đối đỉnh); GM=MD (cm trên); BM=CM (AM là trung tuyến)
-> tam giác BDM = tam giác CGM(c.g.c)
-> BD=CG (dpcm)

Bài 1:
Ta có: ΔABC cân tại A
mà AH là đường cao
nên AH là đường trung tuyến
Xét ΔABC có
AH là đường trung tuyến
BD là đường trung tuyến
AH cắt BD tại E
Do đó: E là trọng tâm của ΔABC

Gọi AM, BN, CP lần lượt là các đường trung tuyến của ΔABC. Các đường trung tuyến cắt nhau tại G.
Ta có: AG = GD (gt)
AG = 2GM (tính chất đường trung tuyến)
Suy ra: GD = 2GM
Mà GD = GM + MD ⇒ GM = MD
Xét ΔBMD và ΔCMG, ta có:
BM = CM (gt)
∠(BMD) = ∠(CMG) (đối đỉnh)
MD = GM (chứng minh trên)
Suy ra: ΔBMD = ΔCMG (c.g.c)
⇒ BD = CG (hai cạnh tương ứng)
Mặt khác: CG = 2/3 CP (tính chất đường trung tuyến)
Suy ra: BD = 2/3 CP (1)
Lại có: BG = 2/3 BN (tính chất đường trung tuyến) (2)
Và AG = 2/3 AM (tính chất đường trung tuyến)
Suy ra: GD = 2/3 AM (3)
Từ (1), (2) và (3) suy ra các cạnh của tam giác BGD bằng 2/3 các đường trung tuyến của tam giác ABC.
\(BM=\dfrac{1}{2}BC\)
\(GE=\dfrac{1}{2}AB\)
DF=AC