Cho hinh thang ABCD có góc A=góc C=90 dộ.AD=AB=2cm. DC=4cm. Tính các góc của hình thang dó
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án cần chọn là: D
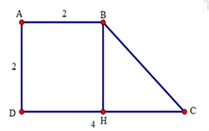
Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.
Lại có B H C ^ = 90 ° (do BH ⊥ CD) nên tam giác BHC vuông cân tại H.
Do đó B C H ^ = 180 ° - B H C ^ ÷ 2 = 180 ° - 90 ° ÷ 2 = 45 °
Xét hình thang ABCD có:
A B C ^ = 360 ° - A ^ + D ^ + C ^ = 360 ° - 90 ° + 90 ° + 45 ° = 135 °
Vậy A B C ^ = 135 ° .

Lấy K là trung điểm của CD , I là trung điểm của DN
Chứng minh tứ giác ABKD là hình vuông
=> ˆADB=45o(1)ADB^=45o(1)
Chứng minh △ DBC△ DBC là tam giác vuông cân =>ˆDBC=90o(2)=>DBC^=90o(2)
Từ (1) và (2) ta được ˆABC=135oABC^=135o
Ta có △ DBN△ DBN vuông tại B có BI là trung tuyến nên BI =DI =IN (3)
lại có △ DMN△ DMN vuông tại M có MI là trung tuyến nên MI= DI =IN(4)
Kết hợp (3)(4) ta có +△ MIB+△ MIB cân tại I nên ˆIMB=ˆIBMIMB^=IBM^(5)
+△ OIN+△ OINcân tại I nên ˆIBN=ˆBNI(6)IBN^=BNI^(6)
Từ (5) (6) ta được : ˆIBM+ˆIBN+ˆIMB+ˆBNI=270oIBM^+IBN^+IMB^+BNI^=270o
=>ˆMIN=360o−270o=90o=>MIN^=360o−270o=90o
=>MI⊥ DN=>MI⊥ DN
Tam giác vuông DMN có MI vừa là tt vừa là đường cao nên là tam giác vuông cân

Lấy K là trung điểm của CD , I là trung điểm của DN
Chứng minh tứ giác ABKD là hình vuông
=> ˆADB=45o(1)ADB^=45o(1)
Chứng minh △ DBC△ DBC là tam giác vuông cân =>ˆDBC=90o(2)=>DBC^=90o(2)
Từ (1) và (2) ta được ˆABC=135oABC^=135o
Ta có △ DBN△ DBN vuông tại B có BI là trung tuyến nên BI =DI =IN (3)
lại có △ DMN△ DMN vuông tại M có MI là trung tuyến nên MI= DI =IN(4)
Kết hợp (3)(4) ta có +△ MIB+△ MIB cân tại I nên ˆIMB=ˆIBMIMB^=IBM^(5)
+△ OIN+△ OINcân tại I nên ˆIBN=ˆBNI(6)IBN^=BNI^(6)
Từ (5) (6) ta được : ˆIBM+ˆIBN+ˆIMB+ˆBNI=270oIBM^+IBN^+IMB^+BNI^=270o
=>ˆMIN=360o−270o=90o=>MIN^=360o−270o=90o
=>MI⊥ DN=>MI⊥ DN
Tam giác vuông DMN có MI vừa là tt vừa là đường cao nên là tam giác vuông cân
thay đổi thông tin đi

Kẻ BH ⊥ CD
Ta có: AD ⊥ CD ( Vì ABCD là hình thang vuông có ∠ A = ∠ D = 90 0 )
Suy ra: BH // AD
Hình thang ABHD có hai cạnh bên song song nên HD = AB và BH = AD
AB = AD = 2cm (gt)
⇒ BH = HD = 2cm
CH = CD – HD = 4 – 2 = 2 (cm)
Suy ra: ∆ BHC vuông cân tại H
Hình đây ạ !!:


