Chứng minh rằng tam giác ABC có cạnh huyền BC = 2a. Goi AH là đường cao của tam giác, D và E là hình chiếu của H trên Ac và Ab. Tìm giá trị lớn nhất của:
a) Độ dài DE.
b*) Diện tích tứ giác ADHE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CH
Cô Hoàng Huyền
Admin
VIP
5 tháng 7 2016
Ta thấy ngay DE = AH do EHDA là hình chữ nhật.
Gọi độ dài hai cạnh góc vuông lần lượt là x và y, khi đó ta có: \(AH=\frac{xy}{2a}\le\frac{x^2+y^2}{4a}=\frac{4a^2}{4a}=a\)
Vậy độ dài lớn nhất của DE là a, khi tam giác ABC vuông cân tại A.
CM
1 tháng 11 2017
Xét hai tam giác vuông ABH và CAH có:
∠ ABH = ∠ CAH (cùng phụ với góc ∠ BAH)
Do đó △ ABH đồng dạng △ CAH (g.g).
Suy ra: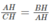 
⇒ A H 2 = BH. CH = 4.9 = 36 ⇒ AH = 6(cm)
Mặt khác, HD ⊥ AB và HE ⊥ AC nên ADHE là hình chữ nhật.
Suy ra: DE = AH = 6 (cm)
26 tháng 8 2022
Câu 1:
a: Xét ΔAHB vuông tạiH có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)
b: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
\(AH=\dfrac{4\cdot6}{2\sqrt{13}}=\dfrac{12}{\sqrt{13}}\left(cm\right)\)
\(AE=\dfrac{AH^2}{AC}=\dfrac{144}{13}:6=\dfrac{24}{13}\left(cm\right)\)
CH
Cô Hoàng Huyền
Admin
VIP
28 tháng 2 2018
a) Xét tam giác AHD và tam giác ABH có:
Góc A chung
\(\widehat{ADH}=\widehat{AHB}\left(=90^o\right)\)
\(\Rightarrow\Delta AHD\sim\Delta ABH\left(g-g\right)\)
\(\Rightarrow\frac{AH}{AB}=\frac{AD}{AH}\Rightarrow AH^2=AB.AD\)
b) Ta có tứ giác ADHE có 3 góc vuông nên nó là hình chữ nhật.
Vậy thì \(\widehat{DHA}=\widehat{DEA}\)
Lại có \(\widehat{DHA}=\widehat{CBA}\) nên \(\widehat{DEA}=\widehat{CBA}\)
Suy ra \(\Delta ADE\sim\Delta ACB\left(g-g\right)\)
c) Gọi I là giao điểm của AO và DE.
Xét tam giác vuông ABC có AO là trung tuyến ứng với cạnh huyền nên OA = OC hay \(\widehat{OAC}=\widehat{OCA}\)
Lại có \(\widehat{AED}=\widehat{ABC}\) nên \(\widehat{OAC}+\widehat{DEA}=\widehat{OCA}+\widehat{ABC}=90^o\)
Suy ra \(\widehat{AIE}=90^o\) hay \(AO\perp DE\)
d) Ta có do \(AO\perp DE\) nên:
\(S_{ADOE}=\frac{1}{2}DE.OA=\frac{1}{2}AH.\frac{BC}{2}=\frac{1}{2}a.AH\)
Vậy thì \(S_{ADOE}\) lớn nhất khi AH lớn nhất.
Xét tam giác vuông ABC, ta có
\(BC.AH=AB.AC\le\frac{AB^2+AC^2}{2}=\frac{BC^2}{2}=2a^2\)
\(\Rightarrow AH\le a\)
Vậy AH lớn nhất khi AH = a tức là tam giác ABC vuông cân tại A.
CM
8 tháng 10 2019
Vì ADHE là hình chữ nhật nên OD = OH
Suy ra, tam giác ODH cân tại O ⇒ ∠ ODH = ∠ OHD
Mà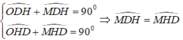 
Xét tam giác MBD có:
∠ (MDB) = ∠ (MBD) (vì cùng phụ với hai góc bằng nhau ∠ (MDH) = ∠ (MHD))
Suy ra, tam giác MBD cân tại M, do đó MD = MB (2)
Từ (1) và (2) suy ra, MB = MH
Vậy M là trung điểm của BH
Tương tự, ta cũng có N là trung điểm của CH.