Câu 9:
Số dư của 20 + 21 + 22 +..... + 2100 khi chia cho 15 là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có A=20+21+22+23+...2100
2A=21+22+...+2101
2A-A=(21+22+...+2100)-(20+21+...+2100)
A=2101-1
Mà 2101-1=(........02)-1=........01 chia 100 dư 1
Chúc bạn học tốt.

Ta có
2 1 + 2 2 + 2 3 + 2 4 + 2 5 + 2 6 + 2 7 +...+ 2 98 + 2 99 + 2 100
= 2 1 + ( 2 2 + 2 3 + 2 4 ) + ( 2 5 + 2 6 + 2 7 ) +...+ ( 2 98 + 2 99 + 2 100 )
= 2 + 2 2 1 + 2 + 2 2 + 2 5 1 + 2 + 2 2 + . . . + 2 98 1 + 2 + 2 2
= 2 + 2 2 . 7 + 2 5 . 7 + . . . + 2 98 . 7 = 2 + 7 2 2 + 2 5 + . . . + 2 98
Mà 7 . 2 2 + 2 5 + . . . + 2 98 ⋮ 7
Nên 2 + 7 2 2 + 2 5 + . . . + 2 98 : 7 d ư 2

A=20+21+22+23+(24+25+..+31) + (32+33+...+39)+...+ (21009+21010+...+21015)+21016
A=80+6+21016+(24+25+..+31) + (32+33+...+39)+...+ (21009+21010+...+21015)
Ta thấy mỗi dấu ngoặc là 8 số tự nhiên liên tiếp có số dư lần lượt là 0,1,2,..,7 có 0+1+2+...+7=28
Số số hạng được chứa trong dấu ngoặc là: (21015-24):1+1=20992 số
Số cặp đó là: 20992:8=2624 Cặp
Do vậy số dư của A chia 8 bằng số dư của B=6+28.2624 (do 80 và 21016 \(⋮\)8)
Mà 2624\(⋮\)8
Nên số dư của A cho 8 là 6
P/S: Bài này em có thể tính tổng ra rồi chia nhưng sẽ cồng kềnh

\(A=1+2+2^2+2^3+...+2^{100}\)
\(=1+\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{99}+2^{100}\right)\)
\(=1+2\left(1+2\right)+2^3\left(1+2\right)+...+2^{99}\left(1+2\right)\)
\(=1+3\left(2+2^3+...+2^{99}\right)\)
=>A chia 3 dư 1

A=(1+2+2^2)+2^3(1+2+2^2)+...+2^2013(1+2+2^2)+2^2016
=7(1+2^3+...+2^2013)+2^2016
Vì 2^2016 chia 7 dư 1
nên A chia 7 dư 1
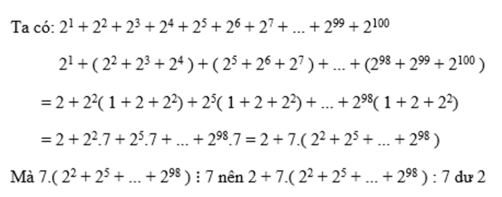


\(A=2^0+2^1+2^2+.....+2^{100}\)
\(\Rightarrow A=2A-A=1-2^{101}\)
\(\Rightarrow A:15=..............\)dư 1