cứu mình phần hình học với ạ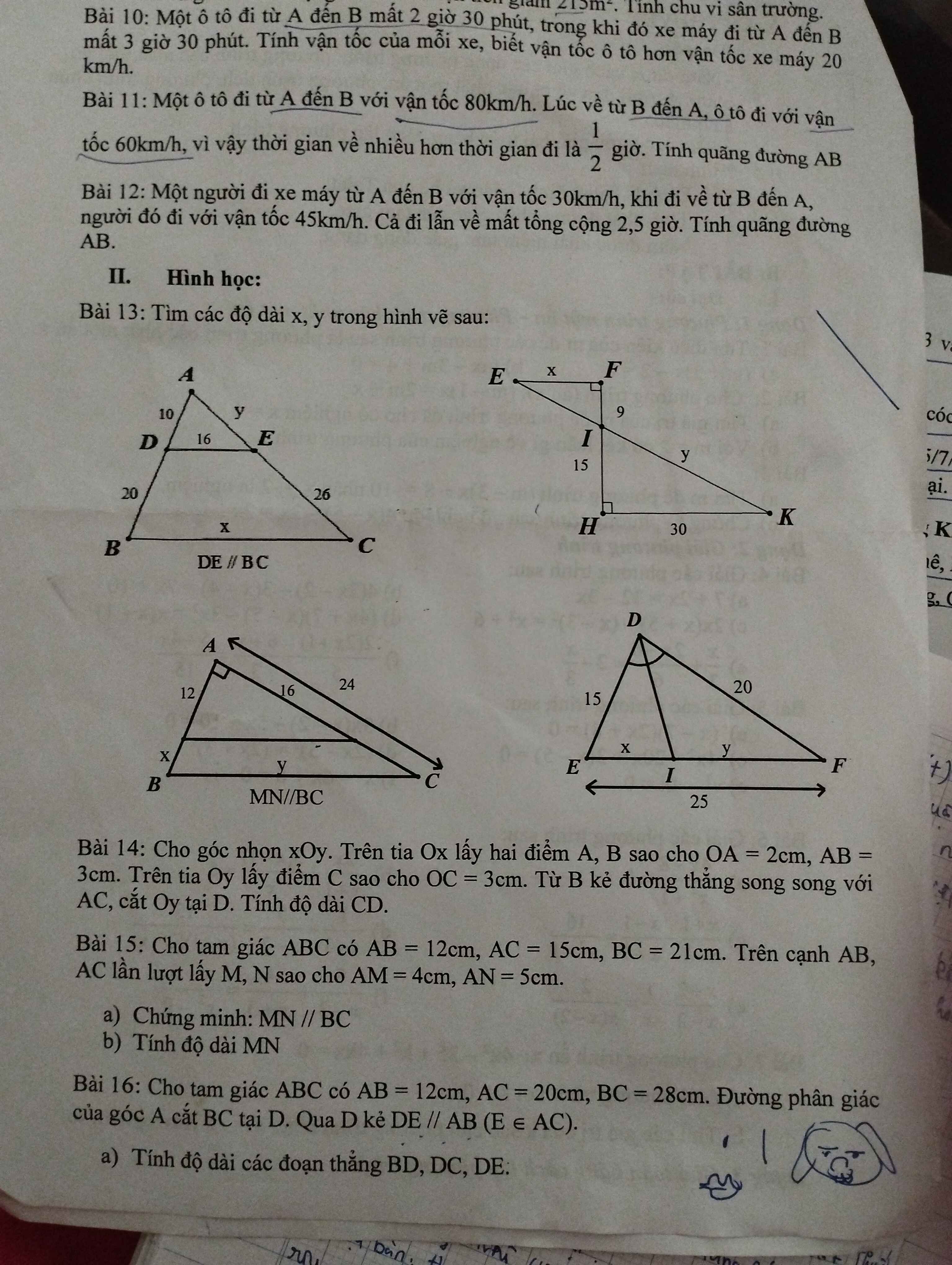
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


#include <bits/stdc++.h>
using namespace std;
int A[50],i,n,ln;
int main()
{
cin>>n;
for (int i=1; i<=n; i++) cin>>A[i];
ln=INT_MIN;
for (int i=1; i<=n; i++)
if (A[i]%2==0 && ln<=A[i]) ln=A[i];
cout<<ln;
}

Bạn cần viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.

1. Bữa sáng:
- Bánh mì: 65gam + Kẹp 20g thịt gà xé
- Sữa đặc có đường: 15gam
2. Bữa trưa:
- Cơm(gạo tẻ): 250gam
--Thịt Gà Ta : 200g
- 1 trái trứng luộc(hay chiên)
3. Bữa tối:
- Cơm(gạo tẻ): 220gam
- Cá chép: 100gam
- Rau muống: 200gam
Ví dụ: Lượng thức ăn của một nữ sinh lớp 8 ăn trong một ngày
1. Bữa sáng:
- Bánh mì: 65gam
- Sữa đặc có đường: 15gam
2. Bữa trưa:
- Cơm(gạo tẻ): 200gam
- Đậu phụ: 75gam
- Thịt lợn ba chỉ: 100gam
- Dưa cải muối: 100gam
3. Bữa tối:
- Cơm(gạo tẻ): 200gam
- hạt ( 200 g)
- Rau muống: 200gam

3:
b: x1^2+x2^2=12
=>(x1+x2)^2-2x1x2=12
=>(2m+2)^2-4m=12
=>4m^2+4m+4=12
=>m^2+m+1=3
=>(m+2)(m-1)=0
=>m=1;m=-2
2:
b: =>|x1|-|x2|=m+3-|-1|=m+2
=>x1^2+x2^2-2|x1x2|=m+2
=>(x1+x2)^2-2x1x2-2|x1x2|=m+2
=>(2m)^2-2(-1)-2|-1|=m+2
=>4m^2-m-2=0
=>m=(1+căn 33)/8; m=(1-căn 33)/8

Đề 1:
A B C D E F M N H
a) Xét tứ giác BDHF có: \(\widehat{BDF}+\widehat{BHF}=90^o+90^o=180^o\)
=> Tứ giác BDHF nội tiếp đường tròn
b) Xét tứ giác BFEC có: \(\widehat{BFC}=\widehat{BEC}=90^o\) => BFEC là tứ giác nội tiếp
=> \(\widehat{BCF}=\widehat{BEF}\) (cùng nhìn cạnh BF) hay \(\widehat{BCN}=\widehat{BEF}\)
Xét đường tròn (O) có \(\widehat{BCN}=\widehat{BMN}\) (cùng chắn \(\stackrel\frown{BN}\)) => \(\widehat{BEF}=\widehat{BMN}\)
Mà 2 góc ở vị trí đồng vị => MN//EF
c) BDHF là tứ giác nội tiếp (cmt) => \(\widehat{DBH}=\widehat{DFH}\) (cùng nhìn cạnh DH)
BFEC là tứ giác nội tiếp (cmt) => \(\widehat{CBE}=\widehat{CFE}\) (cùng nhìn cạnh CE)
hay \(\widehat{DBH}=\widehat{HFE}\) => \(\widehat{DHF}=\widehat{HFE}\left(=\widehat{DBH}\right)\)=> FH là phân giác \(\widehat{DFE}\)
CMTT => EH là phân giác \(\widehat{DEF}\)
Xét ΔDEF có H là giao điểm 2 đường phân giác => H là tâm đường tròn nội tiếp ΔDEF
Đề 2:
M A O B E F I 1 1 1
a) Xét tứ giác MAOB có: \(\widehat{MAO}+\widehat{MBO}=90^o+90^o=180^o\)
=> Tứ giác MAOB nội tiếp đường tròn
b) Xét đường tròn (O) có: \(\widehat{IBF}=\widehat{A_1}\) (cùng chắn \(\stackrel\frown{BF}\))
Xét ΔIBF và ΔIAB có: \(\widehat{AIB}\) chung; \(\widehat{IBF}=\widehat{A_1}\) (cmt) => ΔIBF ~ ΔIAB (g.g)
=> \(\dfrac{IB}{IA}=\dfrac{IF}{IB}\) => IB2 = IF.IA (1)
c) Do AE // MB (gt) => \(\widehat{E_1}=\widehat{M_1}\) (2 góc so le trong)
Xét đường tròn (O) có \(\widehat{E_1}=\widehat{FAM}\) (cùng chắn \(\stackrel\frown{AF}\)) => \(\widehat{M_1}=\widehat{FAM}\)
Xét ΔIFM và ΔIMA có: \(\widehat{AMI}\) chung; \(\widehat{M_1}=\widehat{FAM}\) (cmt)
=> ΔIFM ~ ΔIMA (g.g) => \(\dfrac{IF}{IM}=\dfrac{IM}{IA}\) => IM2 = IF.IA (2)
Từ (1) và (2) => IB2 = IM2 => IB = IM




\(a))\Delta ABC:\)
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\left(do\dfrac{4}{12}=\dfrac{5}{15}\right).\\ \Rightarrow MN//BC\left(Talet\right).\)
\(b))\Delta ABC:MN//BC\left(cmt\right).\\ \Rightarrow\dfrac{MN}{BC}=\dfrac{AM}{AB}\left(Talet\right).\\ \Rightarrow MN=\dfrac{AM.BC}{AB}=\dfrac{4.21}{12}=7\left(cm\right).\)