Giúp mik giải với ạ!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 3:
a: \(BD=\sqrt{BC^2-DC^2}=4\left(cm\right)\)
b: \(\widehat{A}=180^0-2\cdot70^0=40^0< \widehat{B}\)
nên BC<AC=AB
c: Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
\(\widehat{EBC}=\widehat{DCB}\)
Do đó:ΔEBC=ΔDCB
d: Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)
nên ΔOBC cân tại O
Câu 2
a) Thay y = -2 vào biểu thức đã cho ta được:
2.(-2) + 3 = -1
Vậy giá trị của biểu thức đã cho tại y = -2 là -1
b) Thay x = -5 vào biểu thức đã cho ta được:
2.[(-5)² - 5] = 2.(25 - 5) = 2.20 = 40
Vậy giá trị của biểu thức đã cho tại x = -5 là 40


Câu 1:
a)2x-3=5
\(\leftrightarrow\)2x=5+3
\(\leftrightarrow\)2x=8
\(\leftrightarrow\)x=4
Vậy pt có tập nghiệm S={4}
b)(2x+1)(x-3)=0
\(\leftrightarrow\) 2x+1=0
Hoặc x-3=0
\(\leftrightarrow\)x=-1/2
x=3
Vậy pt có tập nghiệm S={-1/2;3}
d)3x-4=11
\(\leftrightarrow\)3x=11+4
\(\leftrightarrow\)3x=15
\(\leftrightarrow\)x=5
Vậy pt có tập nghiệm S={5}
e)(2x-3)(x+2)=0
\(\leftrightarrow\)2x-3=0
Hoặc x+2=0
\(\leftrightarrow\)x=3/2
hoặc x=-2
Vậy pt có tập nghiệm S={3/2;-2}
Câu 2:
a)2x-3<15
\(\leftrightarrow\)2x<15+3
\(\leftrightarrow\)2x<18
\(\leftrightarrow\)x<9
Vật bpt có tập nghiệm S={x|x<9}
c)5x-2<18
\(\leftrightarrow\)5x<20
\(\leftrightarrow\)x<4
Vậy bpt có tập nghiệm S={x|x<4}
Mấy bài phân số nhác gõ quá~



Câu 4:
a: Xét ΔABH vuông tại H và ΔACH vuông tại H có
AB=AC
AH chung
Do đó: ΔABH=ΔACH
b: Xét ΔADH vuông tại D và ΔAEH vuông tại E có
AH chung
\(\widehat{DAH}=\widehat{EAH}\)
Do đó: ΔADH=ΔAEH
Suy ra:HD=HE

Độ dãn của lò xo:
\(F_{đh}=k\cdot\Delta l\Rightarrow\Delta l=\dfrac{F_{đh}}{k}=\dfrac{2}{100}=0,02\)m=2cm

Câu 5:
\(\dfrac{13}{6}+x=-2,4\)
\(\Rightarrow\dfrac{13}{6}+x=-\dfrac{12}{5}\)
\(\Rightarrow x=-\dfrac{12}{5}-\dfrac{13}{6}\)
\(\Rightarrow x=-\dfrac{137}{30}\)
Câu 6:
\(3,7-x=\dfrac{7}{10}\)
\(\Rightarrow\dfrac{37}{10}-x=\dfrac{7}{10}\)
\(\Rightarrow x=\dfrac{37}{10}-\dfrac{7}{10}\)
\(\Rightarrow x=3\)
Câu 7:
\(\dfrac{3}{7}+x=\dfrac{2}{14}\)
\(\Rightarrow\dfrac{3}{7}+x=\dfrac{1}{7}\)
\(\Rightarrow x=\dfrac{1}{7}-\dfrac{3}{7}\)
\(\Rightarrow x=-\dfrac{2}{7}\)
Câu 8:
\(\dfrac{3}{7}\cdot y=\dfrac{-2}{5}\)
\(\Rightarrow y=\dfrac{-2}{5}:\dfrac{3}{7}\)
\(\Rightarrow y=\dfrac{-2}{5}\cdot\dfrac{7}{3}\)
\(\Rightarrow y=-\dfrac{14}{15}\)


 giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ
giúp mik với ạ mik cần gấp. GIẢI CỤ THỂ GIÚP MIK vs ạ

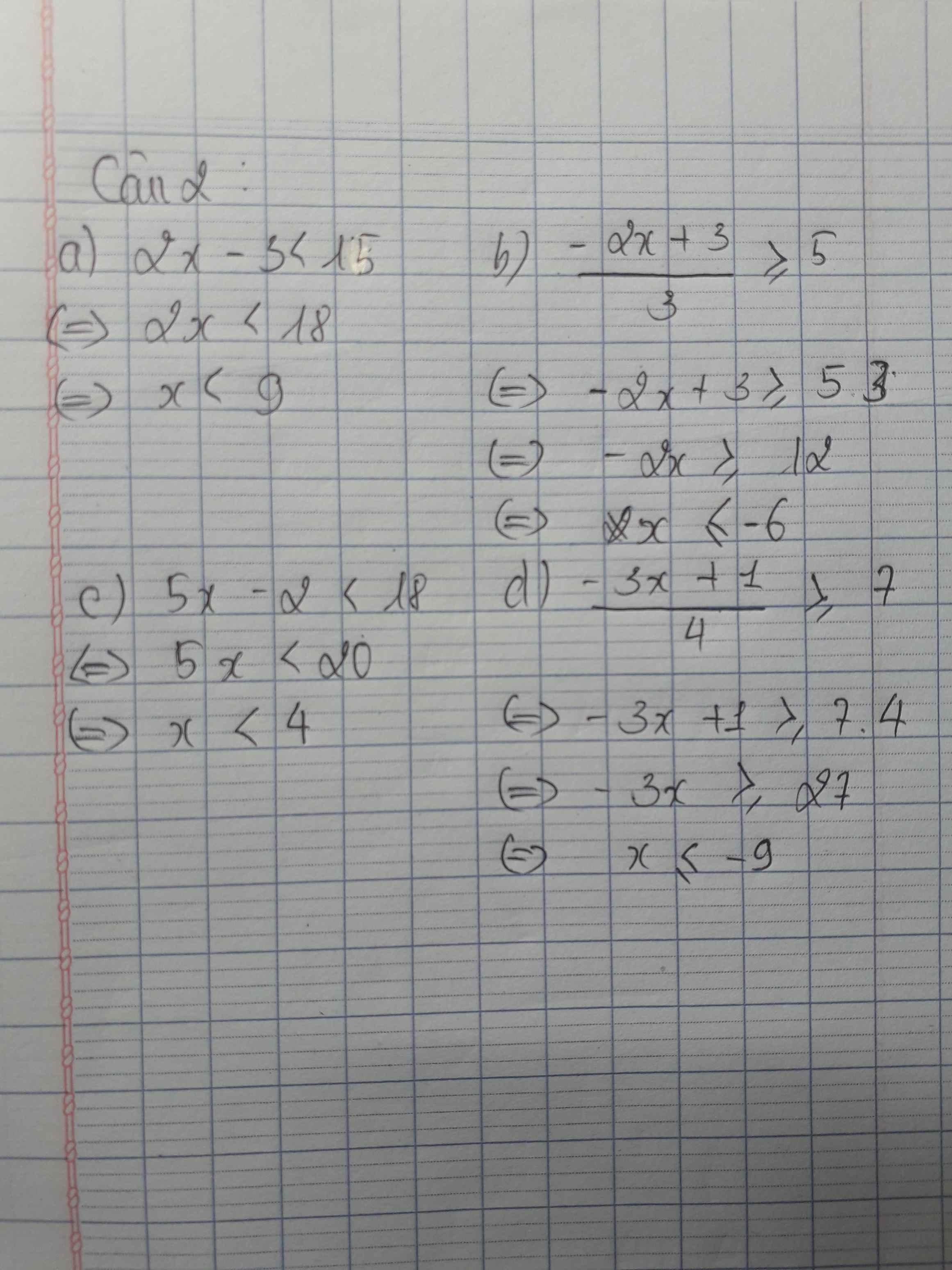




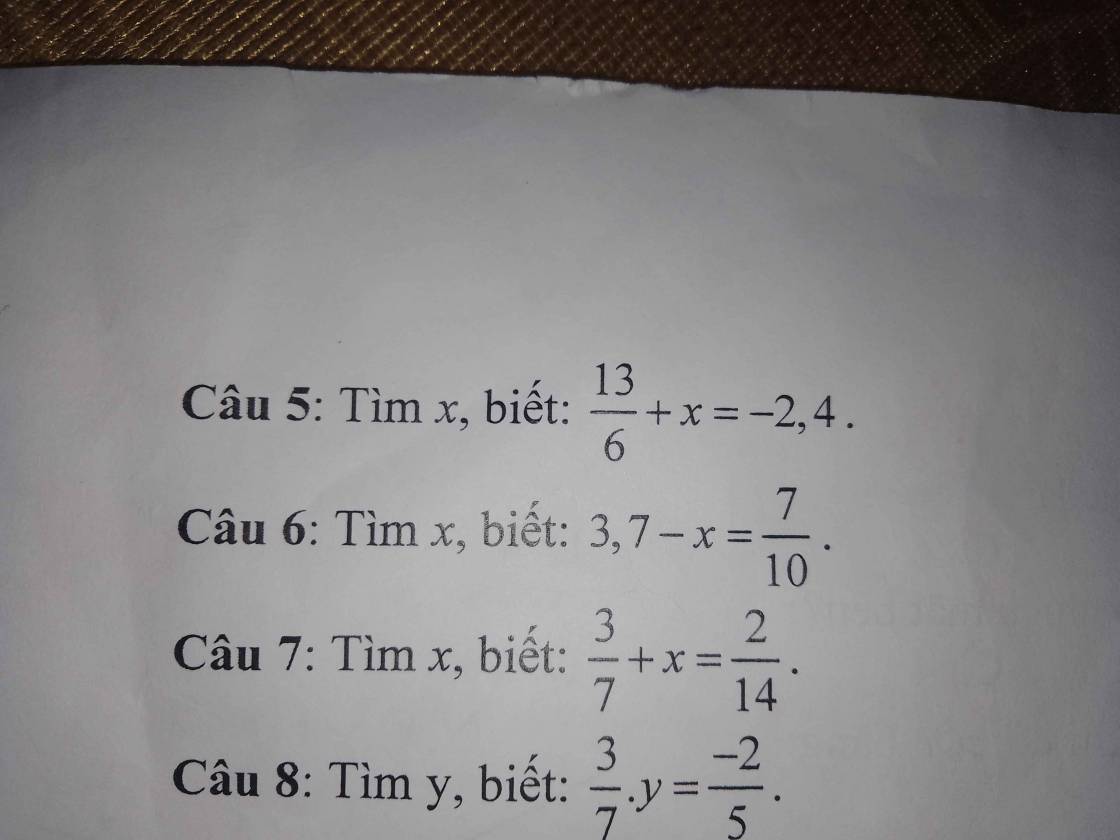
a.
Theo tính chất lập phương, \(CC'\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của \(AC'\) lên (ABCD)
\(\Rightarrow\widehat{C'AC}\) là góc giữa AC' và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=4\sqrt{2}\)
\(\Rightarrow tan\widehat{C'AC}=\dfrac{CC'}{AC}=\dfrac{1}{\sqrt{2}}\Rightarrow\widehat{C'AC}\approx35^016'\)
b.
Theo t/c lập phương, \(CD\perp\left(BCB'\right)\)
Mà CD là giao tuyến (A'B'CD) và (ABCD)
\(\Rightarrow\widehat{BCB'}\) là góc giữa (A'B'CD) và (ABCD)
\(tan\widehat{BCB'}=\dfrac{BB'}{BC}=\dfrac{4}{4}=1\Rightarrow\widehat{BCB'}=45^0\)
c.
\(AA'\perp\left(A'B'C'D'\right)\Rightarrow AA'\perp A'P\Rightarrow\Delta MA'P\) vuông tại A'
\(\Rightarrow MP=\sqrt{A'M^2+A'P^2}=\sqrt{A'M^2+A'D'^2+D'P^2}\)
\(=\sqrt{2^2+4^2+2^2}=2\sqrt{6}\left(cm\right)\)
Tương tự:
\(MN=\sqrt{AM^2+AB^2+BN^2}=2\sqrt{6}\left(cm\right)\)
\(NP=\sqrt{C'P^2+C'C^2+CN^2}=2\sqrt{6}\left(cm\right)\)
\(\Rightarrow MN=MP=NP\Rightarrow\Delta MNP\) đều
\(\Rightarrow S_{\Delta MNP}=\dfrac{MN^2\sqrt{3}}{4}=6\sqrt{3}\left(cm^2\right)\)
d.
Gọi Q là trung điểm CD \(\Rightarrow PQ\perp\left(ABCD\right)\)
\(\Rightarrow\Delta ANQ\) là hình chiếu vuông góc của tam giác MNP lên (ABCD)
\(S_{\Delta ANQ}=S_{ABCD}-S_{ADQ}-S_{ABN}-S_{CNQ}\)
\(=AB^2-\dfrac{1}{2}AD.DQ-\dfrac{1}{2}AB.BN-\dfrac{1}{2}CQ.CN\)
\(=4^2-\dfrac{1}{2}.4.2-\dfrac{1}{2}.4.2-\dfrac{1}{2}.2.2=6\left(cm^2\right)\)
\(\Rightarrow cos\alpha=\dfrac{S_{AQN}}{S_{MNP}}=\dfrac{6}{6\sqrt{3}}=\dfrac{1}{\sqrt{3}}\Rightarrow\alpha\approx54^044'\)