(52x.5x+1):5=125
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
14 tháng 12 2017
Đặt t = 5x, ta có (1)⇔ 1/5.t2 + 5t = 250 ⇔ t2 + 25t - 1250 = 0
⇔ t = 25 hoặc t = -50(loại)
⇔ 5x ⇔ x = 2.
1 tháng 2 2017
a). 5x = 125
=>5x = 53
=> x = 3
b) 32x = 81
=> 32x = 34
=> 2x = 4
=> x = 2
c). 52x-3 – 2.52 = 52 .3
=>52x: 53 = 52 .3 + 2.52
=>52x: 53 = 52 .5
=>52x = 52 .5.53
=>52x = 56
=> 2x = 6
=> x=3
1 tháng 2 2017
a) 5x = 125
x = 125 : 5
x = 25
b) 32x = 81
x = 81 : 32
x = 81/ 32
c) 52x - 3 - 2.52 = 52.3
52x - 3 - 104 = 156
x - 3 - 104 = 156 : 52
x - 3 - 104 = 3
x - 3 = 3 + 104
x - 3 = 107
x = 107 + 3
x = 110
Ko chắc lắm , sai thì Sorry nhé . 
LH
2
VN
Võ Ngọc Phương
VIP
18 tháng 12 2023
\(5.5^{2x+2}=125\)
\(=>5^{2x+2}=125:5\)
\(=>5^{2x+2}=25=5^2\)
\(=>2x+2=2\)
\(=>2x=2-2\)
\(=>2x=0\)
\(=>x=0:2\)
\(=>x=0\)
7 tháng 9 2021
\(5^{2x-1}=125\cdot5^4\)
\(\Leftrightarrow2x-1=7\)
hay x=4
PT
1
25 tháng 9 2021
\(5^{2x+1}.5^{x+1}=5^{17}\)
\(\Rightarrow5^{2x+1+x+1}=5^{17}\)
\(\Rightarrow5^{3x+2}=5^{17}\)
\(\Rightarrow3x+2=17\)
\(\Rightarrow3x=15\Rightarrow x=5\)
9 tháng 9 2021
\(5^{2x+1}\cdot5^{2x+2}-5^x\cdot5^{3x+2}=100\)
\(\Leftrightarrow5^{4x+3}-5^{4x+2}=100\)
\(\Leftrightarrow625^x\left(5^3-5^2\right)=100\)
\(\Leftrightarrow625^x=1\)
hay x=0
9 tháng 9 2021
\(\Rightarrow5^{2x+1+2x+2}-5^{x+3x+2}=100\\ \Rightarrow5^{4x+3}-5^{4x+2}=100\\ \Rightarrow5^{4x+2}\left(5-1\right)=100\\ \Rightarrow5^{4x+2}=25=5^2\\ \Rightarrow4x+2=2\Rightarrow x=0\)
25 tháng 10 2023
a: \(4x^3+12=120\)
=>\(4x^3=108\)
=>\(x^3=27=3^3\)
=>x=3
b: \(\left(x-4\right)^2=64\)
=>\(\left[{}\begin{matrix}x-4=8\\x-4=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=12\\x=-4\end{matrix}\right.\)
c: (x+1)^3-2=5^2
=>\(\left(x+1\right)^3=25+2=27\)
=>x+1=3
=>x=2
d: 136-(x+5)^2=100
=>(x+5)^2=36
=>\(\left[{}\begin{matrix}x+5=6\\x+5=-6\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=1\\x=-11\end{matrix}\right.\)
e: \(4^x=16\)
=>\(4^x=4^2\)
=>x=2
f: \(7^x\cdot3-147=0\)
=>\(3\cdot7^x=147\)
=>\(7^x=49\)
=>x=2
g: \(2^{x+3}-15=17\)
=>\(2^{x+3}=32\)
=>x+3=5
=>x=2
h: \(5^{2x-4}\cdot4=10^2\)
=>\(5^{2x-4}=\dfrac{100}{4}=25\)
=>2x-4=2
=>2x=6
=>x=3
i: (32-4x)(7-x)=0
=>(4x-32)(x-7)=0
=>4(x-8)*(x-7)=0
=>(x-8)(x-7)=0
=>\(\left[{}\begin{matrix}x-8=0\\x-7=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=8\\x=7\end{matrix}\right.\)
k: (8-x)(10-2x)=0
=>(x-8)(x-5)=0
=>\(\left[{}\begin{matrix}x-8=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=8\\x=5\end{matrix}\right.\)
m: \(3^x+3^{x+1}=108\)
=>\(3^x+3^x\cdot3=108\)
=>\(4\cdot3^x=108\)
=>\(3^x=27\)
=>x=3
n: \(5^{x+2}+5^{x+1}=750\)
=>\(5^x\cdot25+5^x\cdot5=750\)
=>\(5^x\cdot30=750\)
=>\(5^x=25\)
=>x=2
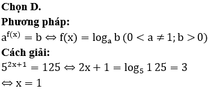
\(\left(5^{2x+x+1}\right)=125.5=625\)
\(5^{3x}.5=625\)
\(5^{3x}=125\)
\(125^x=125\)
\(\Rightarrow x=1\)
(52x.5x+1):5=125
(52x.5x+1)= 125.5
(52x.5x+1)=625
\(5^{3x}=125\Rightarrow125^x=125=>x=1\)