Tìm a và b để phương trình (x-1)a+(2x+1)b=x+2 có tập nghiệm là R
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tập nghiệm của bất phương trình đã cho là đoạn [2a - b + 1; -a + 2b - 1] (nếu 2a - 6 + 1 ≤ -a + 26 - 1) hoặc là đoạn [-a + 26 - 1 ; 2a - 6 + 1] (nếu -a + 2b - 1 ≤ 2a - 6 - 1)
Do đó để tập nghiệm của bất phương trình đã cho là đoạn [0;2], điều kiện cần và đủ là:
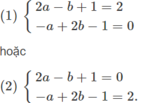
Giải (1) ta được a = b = 1. Giải hệ (2) ta được a = 1/3, b = 5/3
Đáp số: a = b = 1 hoặc a = 1/3, b = 5/3

\(\dfrac{2x}{x^2+1}\ge1\Leftrightarrow2x\ge x^2+1\Leftrightarrow x^2-2x+1\le0\\ \Leftrightarrow\left(x-1\right)^2\le0\)
Mà \(\left(x-1\right)^2\ge0\Leftrightarrow x-1=0\Leftrightarrow x=1\)
\(A=\left\{1\right\}\)
Để \(x^2-2bx+4=0\Leftrightarrow\Delta=4b^2-4\cdot4< 0\)
\(\Leftrightarrow b^2-4< 0\Leftrightarrow\left(b-2\right)\left(b+2\right)< 0\\ \Leftrightarrow x\le-2;x\ge2\)
\(\Leftrightarrow B=\left\{x\in R|x\le-2;x\ge2\right\}\)
Vậy \(A\cap B=\varnothing\)

=>3x^2-c=ax^2-2ax+a-bx+b
=>3x^2-c-a*x^2+2ax-a+bx-b=0
=>x^2(3-a)+x(2a+b)-a-b-c=0
Để phương trình luôn có nghiệm thì 3-a=0 và 2a+b=0 và a+b+c=0
=>a=3; b=-6; c=-a-b=-3+6=3

a: Khi x=-2 thì pt sẽ là;
4+4+m-2=0
=>m+6=0
=>m=-6
=>x^2-2x-8=0
=>(x-4)(x+2)=0
=>x=4 hoặc x=-2
b: 1/x1+1/x2=2
=>(x1+x2)/(x1x2)=2
=>2/(m-2)=2
=>m-2=1
=>m=3

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

1:
a: 2x-3=5
=>2x=8
=>x=4
b: (x+2)(3x-15)=0
=>(x-5)(x+2)=0
=>x=5 hoặc x=-2
2:
b: 3x-4<5x-6
=>-2x<-2
=>x>1
(x-1)a+(2x+1)b=x+2
=>\(x\cdot a-a+2xb+b-x-2=0\)
=>\(x\left(a+2b-1\right)+\left(-a+b-2\right)=0\)
Để phương trình có tập nghiệm là R thì \(\left\{{}\begin{matrix}a+2b-1=0\\-a+b-2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a+2b=1\\-a+b=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3b=3\\a+2b=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=1\\a=1-2b=-1\end{matrix}\right.\)