Cho tam giác CDF cân tại C. Kẻ 𝐶𝐻 ⊥ 𝐷𝐹 (𝐺 ∈ 𝐷𝐹) a) Chứng minh: Δ𝐶𝐻𝐷 = Δ𝐶𝐻𝐹 b) Chứng minh: DH = FH c) Kẻ 𝐻𝑁 ⊥ 𝐶𝐷 (𝑁 ∈ 𝐶𝐷); 𝐻𝑀 ⊥ 𝐶𝐹(𝑀 ∈ 𝐶𝐹). Chứng minh tam giác CNM cân tại C.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



hình tự kẻ:33333
a) xét tam giác BAD và tam giác BHD có
B1=B2(gt)
BD chung
BAD=BHD(=90 độ)
=> tam giác BAD= tam giác BHD(ch-gnh)
=> AB=BH( hai cạnh tương ứng)
b) từ tam giác BAD =tam giácBHD=> AD=AH( hai cạnh tương ứng)
áp dụng điịnh lý pytago vào tam giác vuông HDC=> DC^2=DH^2+HC^2
=> DC^2>DH^2
=>DC^2>AD^2
=> DC>AD
c) xét tam giác BAC và tam giác BHKcó
AB=HB(cmt)
BAC=BHK(=90 độ)
B chung
=> tam giác BAC= tam giác BHK(gcg)
=> AK=AC( hai cạnh tương ứng)
=> tam giác BKC cân B

a: Ta có: ΔECD vuông tại C
=>\(CD^2+CE^2=ED^2\)
=>\(ED^2=5^2+12^2=169\)
=>\(ED=\sqrt{169}=13\left(cm\right)\)
Chu vi tam giác ECD là:
13+12+5=13+17=30(cm)
b: Xét ΔDCF vuông tại C và ΔDHF vuông tại H có
DF chung
\(\widehat{CDF}=\widehat{HDF}\)
Do đó: ΔDCF=ΔDHF
c: Ta có: ΔDCF=ΔDHF
=>FH=FC
mà FH<FE(ΔFHE vuông tại H)
nên FC<FE

Áp dụng Đ. L. py-ta-go vào tg CDE vuông tại C, có:
DE2=CD2+CE2
=>DE2=52+122
=25+144
=169.
=>DE=13cm.
Chu vi tg CDE là:
13+5+12=30(cm)
b, Xét tg DCF và tg DHF, có:
góc CDF= góc FDH(tia phân giác)
DF chung
góc C= góc DHF(=90o)
=>tg DCF= tg DHF(ch-gn)
c, Mik chx làm đc:<

4 bài toàn là hình, lại khó, dài , mk nghĩ chắc ko ai tl giúp bn đâu, xl nha, ngay mk mới lp 6 cx chưa thể giải đc vì đã lp 7 đâu. ah hay là bn gửi tg bài 1 cho các bn ấy giải từ từ, cứ 1 đốg thì ai giải giúp bn đc. sorry nha
*In đậm: quan trọng.

a) Xét ΔABD và ΔACD có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}=\widehat{CAD}\)(AD là tia phân giác của \(\widehat{BAC}\))
AD chung
Do đó: ΔABD=ΔACD(c-g-c)
Suy ra: DB=DC(hai cạnh tương ứng)
b) Xét ΔDBH vuông tại H và ΔDCK vuông tại K có
DB=DC(cmt)
\(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔDBH=ΔDCK(cạnh huyền-góc nhọn)
Suy ra: DH=DK(hai cạnh tương ứng)
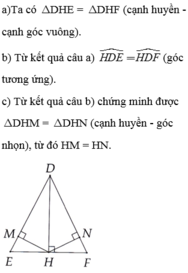
a: Xét ΔCHD vuông tại H và ΔCHF vuông tại H có
CD=CF
CH chung
Do đó: ΔCHD=ΔCHF
b: Ta có: ΔCHD=ΔCHF
nên HD=HF
c: Xét ΔCNH vuông tại N và ΔCMH vuông tại M có
CH chung
\(\widehat{NCH}=\widehat{MCH}\)
Do đó: ΔCNH=ΔCMH
Suy ra: CN=CM
hay ΔCNM cân tại C