Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


3x . 2 + 15 = 33
3x . 2 = 33 - 15 = 18
3x = 18 : 2 = 9 = 32
=> x = 2

\(\dfrac{15}{19}\times\dfrac{25}{33}-\dfrac{15}{19}\times\dfrac{14}{33}\)
\(=\dfrac{15}{19}\times\left(\dfrac{25}{33}-\dfrac{14}{33}\right)\)
\(=\dfrac{15}{19}\times\dfrac{11}{33}\)
\(=\dfrac{5}{19}\)

\(\left|x+\frac{4}{15}\right|-\left|-3,75\right|=-\left|-2,15\right|\)
=> \(\left|x+\frac{4}{15}\right|-3,75=-2,15\)
=> \(\left|x+\frac{4}{15}\right|=-2,15+3,75\)
=> \(\left|x+\frac{4}{15}\right|=1,6=\frac{8}{5}\)
=> \(\orbr{\begin{cases}x+\frac{4}{15}=\frac{8}{5}\\x+\frac{4}{15}=\frac{-8}{5}\end{cases}}\)=> \(\orbr{\begin{cases}x=\frac{4}{3}\\x=\frac{-28}{15}\end{cases}}\)

\(=15x\left(\dfrac{21}{43}+\dfrac{22}{43}\right)=15x1=15\)

a, Vì D là trung điểm BC => OD vuông BC
AM là tiếp tuyến với M là tiếp điểm nên ^AMO = 900
Xét tứ giác AMOD ta có
^AMO + ^ADO = 1800
mà 2 góc này đối
Vậy tứ giác AMOD nt 1 đường tròn
b, Xét tam giác AMB và tam giác ACM ta có
^AMB = ^ACM ( cùng chắn cung MB )
^A _ chung
Vậy tam giác AMB ~ tam giác ACM (g.g)
=> AM/AC = AB/AM => AM^2 = AB.AC
c, bạn ktra lại đề

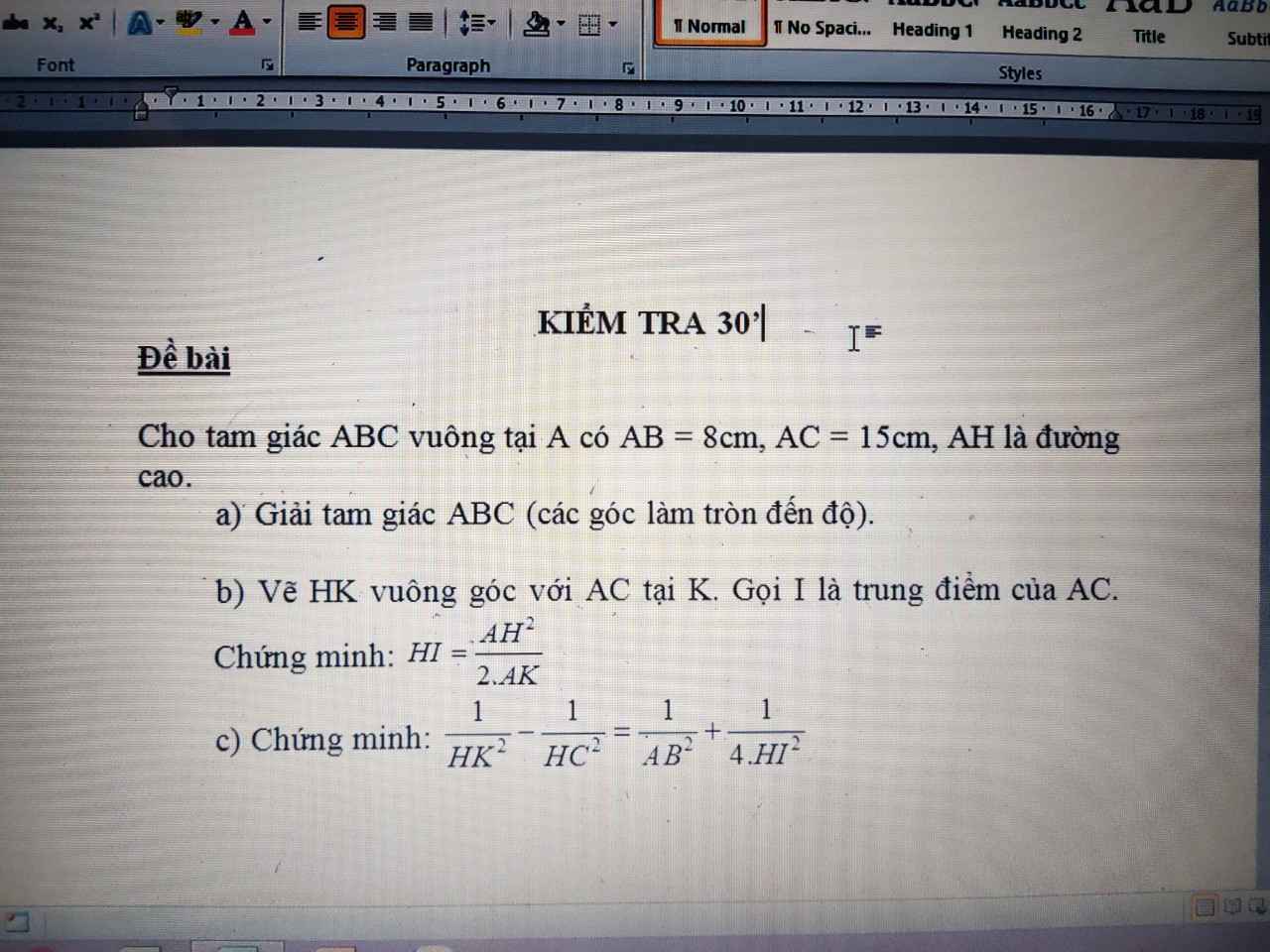
b: Xét ΔAHC vuông tại H có HK là đường cao ứng với cạnh huyền AC
nên \(AH^2=AC\cdot AK\)
\(\Leftrightarrow\dfrac{AC}{2}=\dfrac{AH^2}{2\cdot AK}\)
hay \(HI=\dfrac{AH^2}{2\cdot AK}\)

\(-\left(-x\right):\left(-15\right).2=16\)
\(\Rightarrow x:\left(-15\right)=8\)
\(\Rightarrow x=-120\)
Vậy: \(x=-120\)