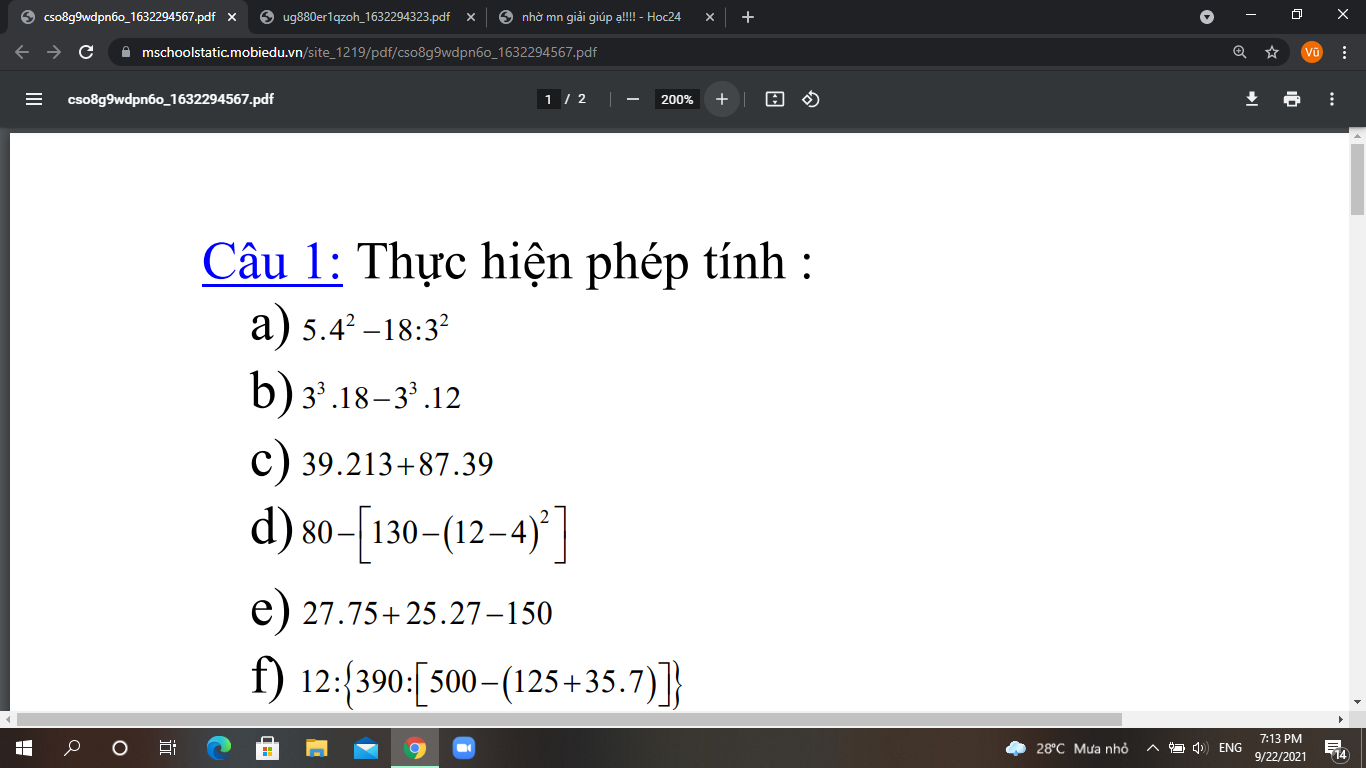
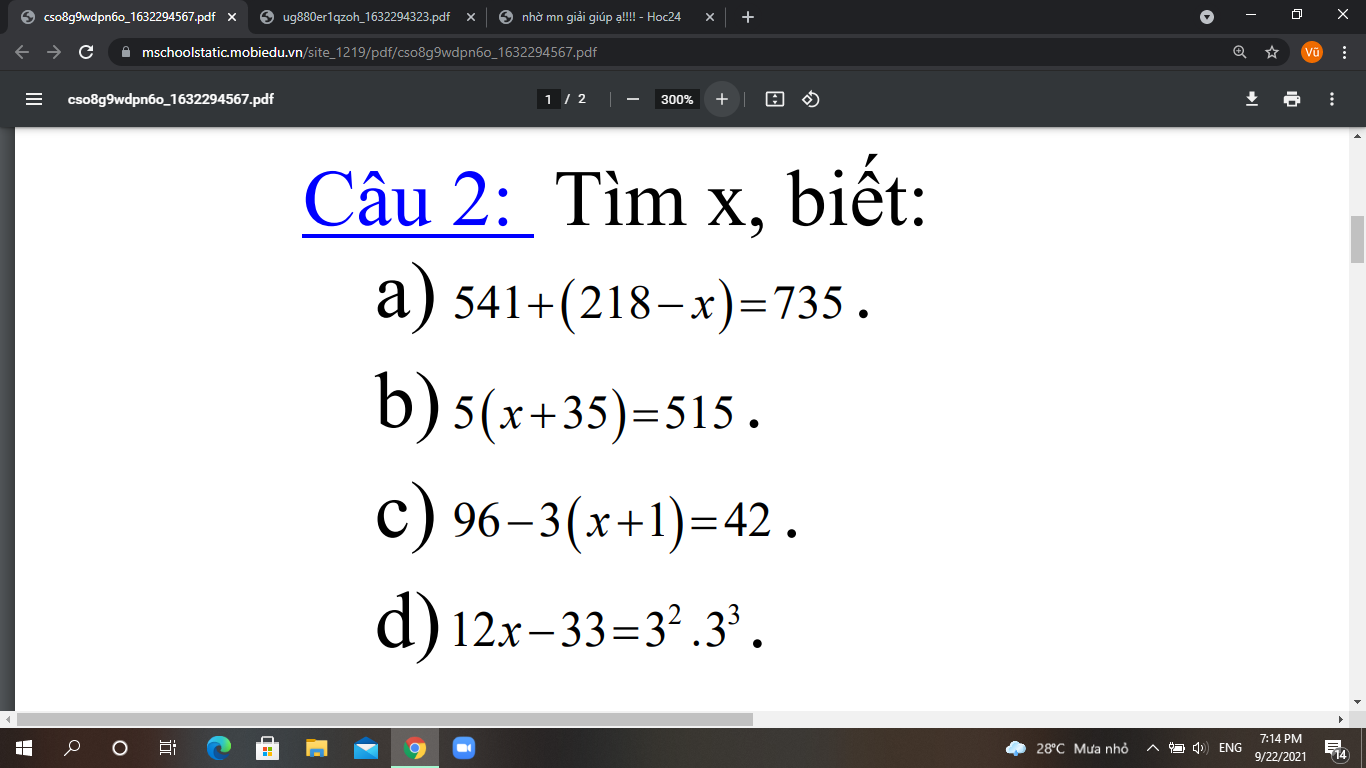
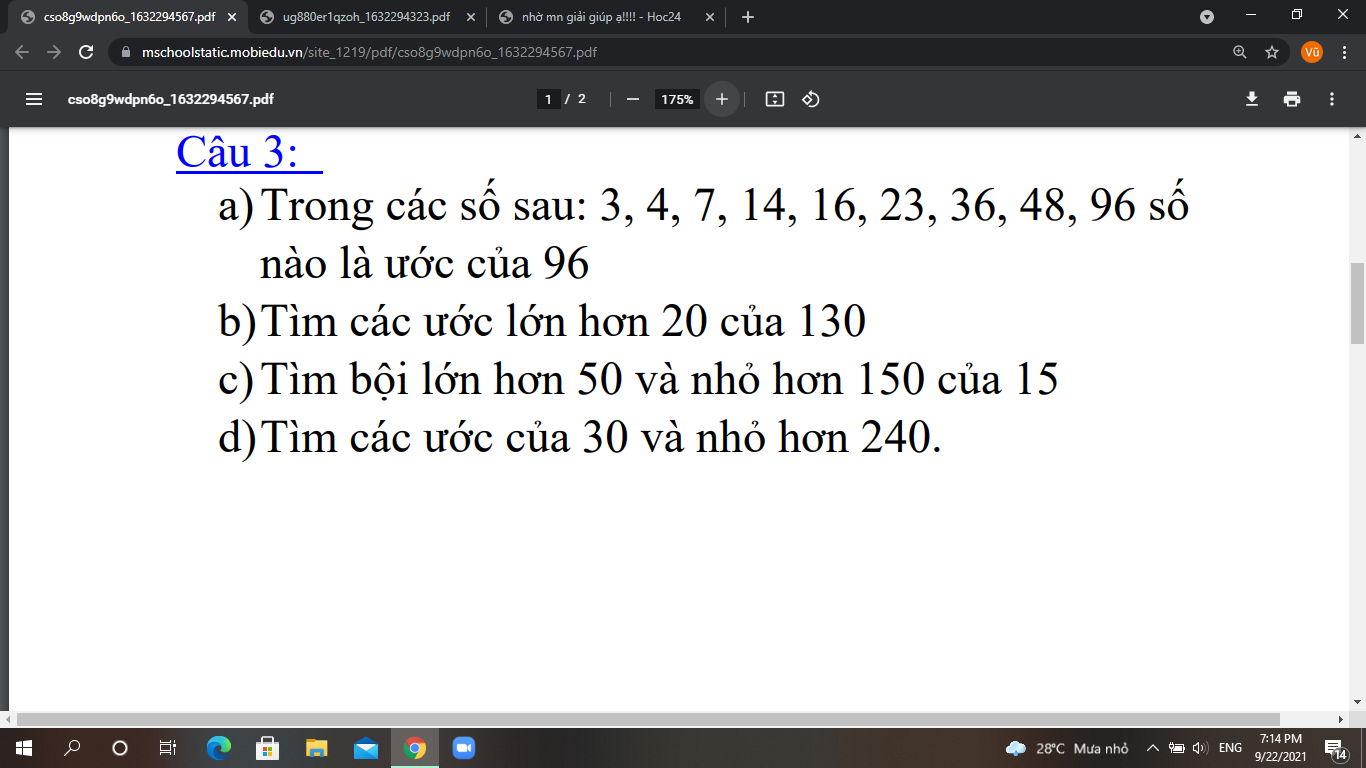
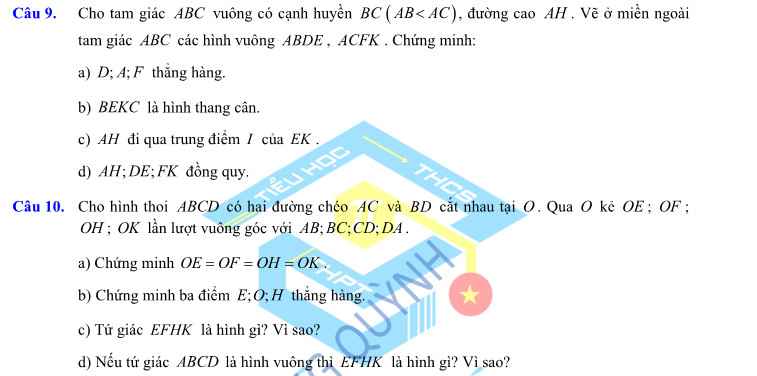
Giúp mik với mn mik đg cần gấp 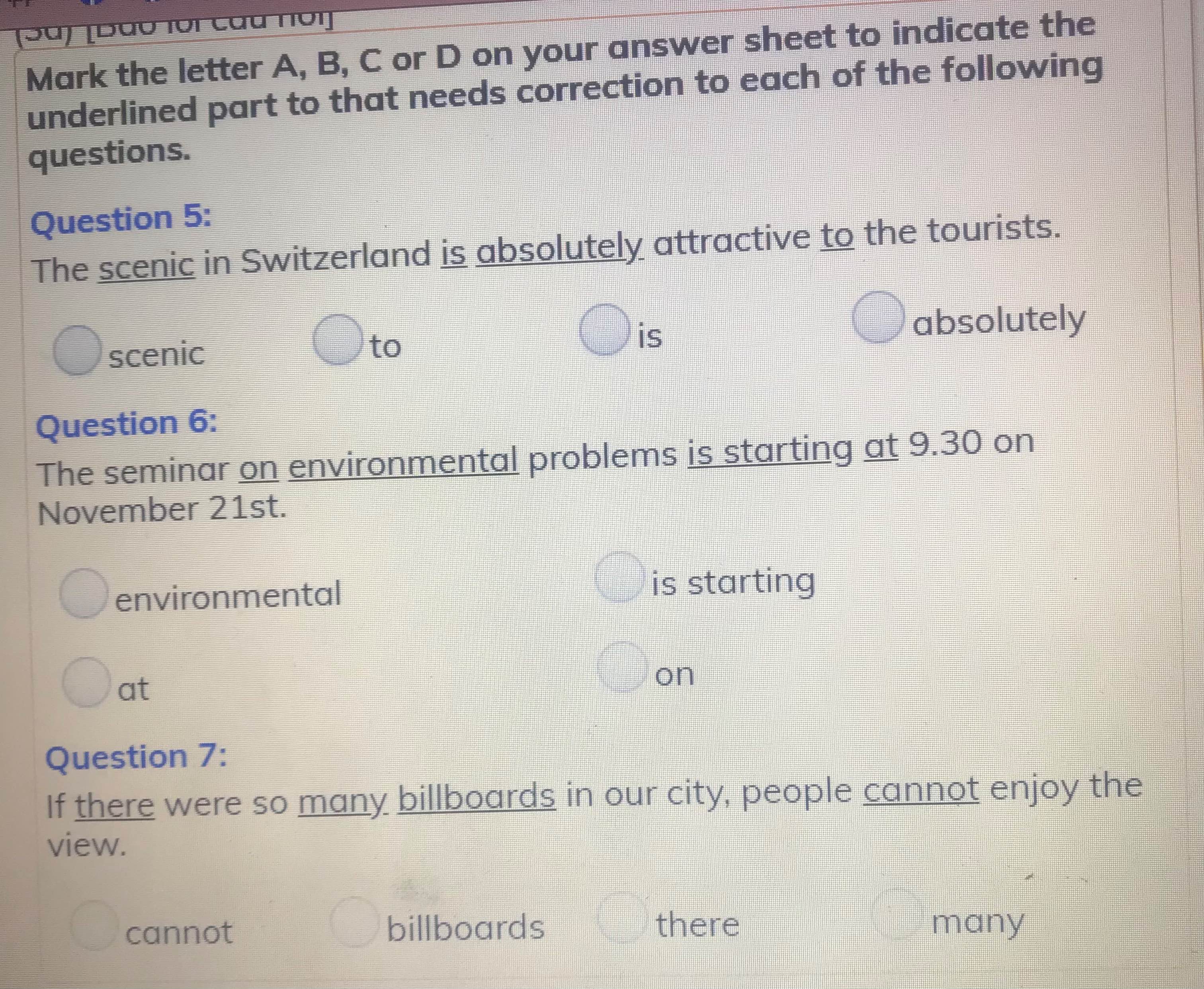
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


đề khó nhìn quá
I.
1A
2C
3A
4C
5B
6B
7C
8B
9B
10C
II.
1T
2F
3F
4T
5F
6T
7F
8T
9F
10F

7:
a: ĐKXĐ: x>=0; x<>1
\(D=\dfrac{1}{2\sqrt{x}-2}-\dfrac{1}{2\sqrt{x}+2}+\dfrac{\sqrt{x}}{1-x}\)
\(=\dfrac{1}{2\left(\sqrt{x}-1\right)}-\dfrac{1}{2\left(\sqrt{x}+1\right)}-\dfrac{\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}+1-\sqrt{x}+1-2\sqrt{x}}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2\left(\sqrt{x}-1\right)}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{-1}{\sqrt{x}+1}\)
b: Khi x=4/9 thì \(D=\dfrac{-1}{\dfrac{2}{3}+1}=-1:\dfrac{5}{3}=-\dfrac{3}{5}\)
c: |D|=1/3
=>D=-1/3 hoặc D=1/3
=>\(\left[{}\begin{matrix}\dfrac{-1}{\sqrt{x}+1}=\dfrac{-1}{3}\\\dfrac{-1}{\sqrt{x}+1}=\dfrac{1}{3}\left(loại\right)\end{matrix}\right.\)
=>\(\sqrt{x}+1=3\)
=>\(\sqrt{x}=2\)
=>x=4
6:
a: \(C=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\right):\left(\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)+x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}:\dfrac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\sqrt{x}-x+x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\)
\(=\dfrac{3\left(\sqrt{x}+3\right)}{3+\sqrt{x}}\cdot\dfrac{-\sqrt{x}}{2\sqrt{x}+4}=\dfrac{-3\sqrt{x}}{2\sqrt{x}+4}\)
b: C<-1
=>C+1<0
=>\(\dfrac{-3\sqrt{x}+2\sqrt{x}+4}{2\sqrt{x}+4}< 0\)
=>\(-\sqrt{x}+4< 0\)
=>\(-\sqrt{x}< -4\)
=>\(\sqrt{x}>4\)
=>x>16
\(C=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{9-x}\right):\left(\dfrac{3\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right)\\ =\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\right):\left(\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{1}{\sqrt{x}}\right)\\ =\left(\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}+\dfrac{x+9}{\left(3-\sqrt{x}\right)\left(3+\sqrt{x}\right)}\right):\left(\dfrac{3\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{\sqrt{x}-3}{\sqrt{x}\left(\sqrt{x}-3\right)}\right)\\ =\dfrac{3\sqrt{x}-x+x+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}:\dfrac{3\sqrt{x}+1-\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{3\sqrt{x}+9}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\\ =\dfrac{3\left(\sqrt{x}+3\right)}{\left(3+\sqrt{x}\right)\left(3-\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(3-\sqrt{x}\right)}{2\sqrt{x}+4}\\ =\dfrac{-3\sqrt{x}}{2\sqrt{x}+4}\)
Để `C < -1` Ta có :
\(\dfrac{-3}{2\sqrt{x}+4}< -1\\ \Leftrightarrow\dfrac{-3}{2\sqrt{x}+4}+1< 0\\ \Leftrightarrow\dfrac{-3}{2\sqrt{x}+4}+\dfrac{2\sqrt{x}+4}{2\sqrt{x}+4}< 0\\ \Leftrightarrow-3+2\sqrt{x}+4< 0\\ \Leftrightarrow2\sqrt{x}+1< 0\\ \Leftrightarrow2\sqrt{x}< -1\\ \Leftrightarrow\sqrt{x}< -\dfrac{1}{2}\\ \Leftrightarrow x< \dfrac{1}{4}\)

Độ dãn của lò xo:
\(F_{đh}=k\cdot\Delta l\Rightarrow\Delta l=\dfrac{F_{đh}}{k}=\dfrac{2}{100}=0,02\)m=2cm

hai bài câu a mik lm đc r nhe mn lm giúp mik câu b thôi ạ mik ko bt lm;-;
Bài 3:
\(a,=-\left(x^2-2x+1\right)-2=-\left(x-1\right)^2-2\le-2\)
Dấu \("="\Leftrightarrow x=1\)
\(b,=-2\left(x^2+2\cdot\dfrac{1}{4}x+\dfrac{1}{16}\right)+\dfrac{9}{8}=-2\left(x+\dfrac{1}{4}\right)^2+\dfrac{9}{8}\le\dfrac{9}{8}\)
Dấu \("="\Leftrightarrow x=-\dfrac{1}{4}\)
Bài 4:
\(a,=\left(x^2+2\cdot\dfrac{5}{2}x+\dfrac{25}{4}\right)-\dfrac{21}{4}=\left(x+\dfrac{5}{2}\right)^2-\dfrac{21}{4}\ge-\dfrac{21}{4}\)
Dấu \("="\Leftrightarrow x=-\dfrac{5}{2}\)
\(b,=\left(x^2-8x+16\right)+1=\left(x-4\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow x=4\)

Bài 5
B= \(\dfrac{2015}{2016+2017+2018}\)+\(\dfrac{2016}{2016+2017+2018}\)+\(\dfrac{2017}{2016+2017+2018}\)
Ta có:\(\dfrac{2015}{2016}\)>\(\dfrac{2015}{2016+2017+2018}\),\(\dfrac{2016}{2017}\)>\(\dfrac{2016}{2016+2017+2018}\),\(\dfrac{2017}{2018}\)>\(\dfrac{2017}{2016+2017+2018}\)
⇒A>B
Bài 5:
Ta có:
\(B=\dfrac{2015+2016+2017}{2016+2017+2018}\)
\(B=\dfrac{2015}{2016+2017+2018}+\dfrac{2016}{2016+2017+2018}+\dfrac{2017}{2016+2017+2018}\)
Vì \(\dfrac{2015}{2016}>\dfrac{2015}{2016+2017+2018}\)
\(\dfrac{2016}{2017}>\dfrac{2016}{2016+2017+2018}\)
\(\dfrac{2017}{2018}>\dfrac{2017}{2016+2017+2018}\)
\(\Rightarrow A>B\)



Câu 4:
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Câu 1:
\(a,=\dfrac{1}{2}+9\cdot\dfrac{1}{9}-18=\dfrac{1}{2}+1-18=-\dfrac{33}{2}\\ b,=2-1+4\cdot\dfrac{1}{4}+9\cdot\dfrac{1}{9}\cdot9=1+1+9=11\\ c,=-21,3\left(54,6+45,4\right)=-21,3\cdot100=-2130\\ d,B=\left(\dfrac{1}{16}+\dfrac{1}{2}-\dfrac{1}{16}\right):\left(\dfrac{1}{8}-\dfrac{1}{8}+1\right)=\dfrac{1}{2}:1=\dfrac{1}{2}\)


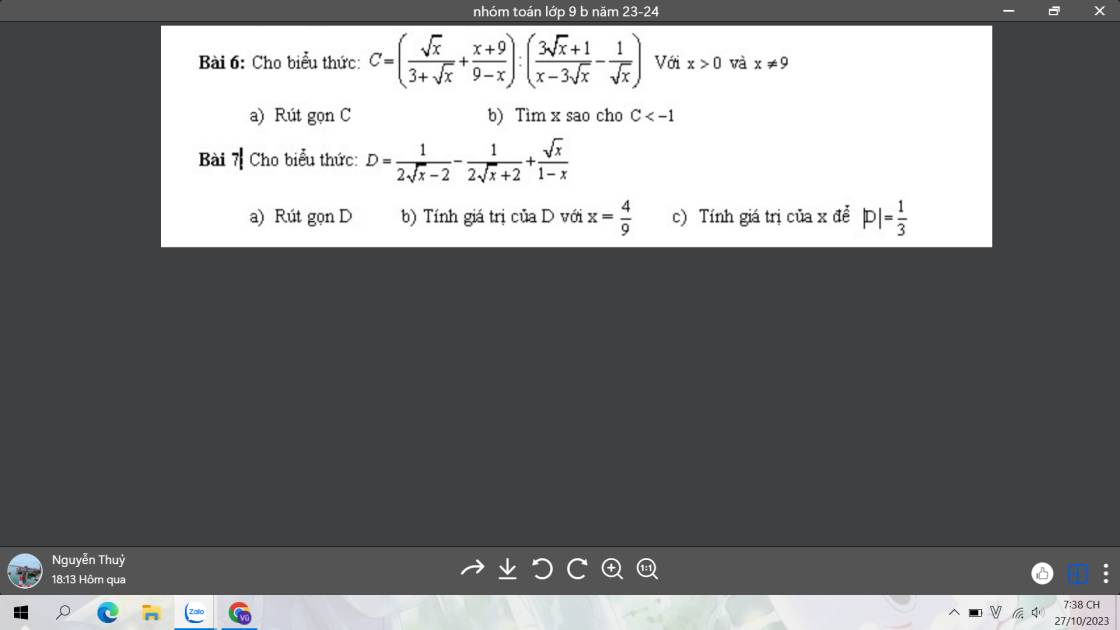 giúp mik với mn ơi mik đg cần gấp
giúp mik với mn ơi mik đg cần gấp