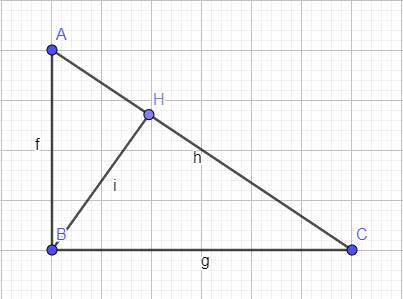
Bài 1. Cho ΔABC vuông góc tại A, đường cao AH (H ∈ BC) và phân giác BE của ABC (E ∈ AC) cắt nhau tại I . Chứng minh rằng:
a) ΔABE ΔHBI.
b) ΔBHA ΔBAC. Rồi suy ra AB2 = BH. BC
c) ΔAIE cân.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.Xét ΔHBA và ΔABC có:
góc AHB=góc BAC=90o
Góc B chung
=> ΔABC đồng dạng ΔHBA (g.g)
=>\(\dfrac{BA}{BH}=\dfrac{BC}{BA}\)\(\Rightarrow BA.BA=BH.BC\)
2. Xét ΔHBI và ΔABE có:
góc ABE=IBH (Vì BE là tia phân giác của góc B, I nằm trên BE)
góc BAE=góc IHB=90o
=>ΔHBI đồng dạng ΔABE (g.g)

a) Xét tam giác BHA và BHE có:
BD chung
ˆABD^=ˆEBD^(vì BD là phân giác ˆBB^)
ˆBHA^=ˆBHE^(vì AH vuông góc với Bd tại H)
⇒Tam giác BHA=tam giac BHE(c.g.v-g.n.k)
b) Xét Tam giác BDA và tam giác BDE có
BD chung
BA=BE( vì tam giac BHA = tam giac BHE( chứng minh phần a))
ABD=EBD( vì BD là phân giác củaˆBB^)
⇒⇒Tam giác BDA = Tam giác BDE(c.g.c)
⇒⇒ˆBEA^=ˆA^= 90o(2 canh tương ứng và ˆA^= 90o)
ED vuông góc với B tại E
c, AD = DE
DE < CD do tam giác CDE vuông tại E
=> AD < DC
d, DA= DE do tam giác ABD = tam giác EBD (Câu b)
=> tam giác DAE cân tại D (đn)
=> ^DAE = ^DEA (tc) (1)
có : AK _|_ BC (gt) ; DE _|_ BC (câu b)
=> DE // AK
=> ^DEA = ^EAK (slt) và (1)
=> ^DAE = ^EAK mà AE nằm giữa AD và AK
=> AE là phân giác của ^CAK (đpcm)
a) Vì EH ⊥ BC ( gt )
=> ΔBHE vuông tại H
Xét tam giác vuông BAE và tam giác vuông BHE có :
BE chung
∠B1 = ∠B2 ( BE là tia phân giác của ∠BAC )
=> ΔBAE = ΔBHE ( cạnh huyền - góc nhọn )
b) Gọi I là giao điểm của AH và BE
Xét ΔABI và ΔHBI có :
BA = BH (ΔBAE = ΔBHE (cmt)
∠B1 = ∠B2 ( BE là tia phân giác của ∠BAC )
BI chung
=> ΔABI = ΔHBI ( c.g.c )
=> ∠AIB = ∠AIH ( 2 góc tương ứng )
Mà ∠AIB + ∠AIH = 1800 ( 2 góc kề bù )
=> ∠AIB = ∠AIH = 900
=> BI ⊥ AH (1)
Ta có: IA = IH ( ΔABI = ΔHBI ( cmt )
Mà I nằm giữa hai điểm A và H (2)
=> I là trung điểm của AH ( 3)
Từ (1) (2) (3) => BI là trung trực của AH
Hay BE là trung trực của AH
c) Xét ΔKAE và ΔCHE có:
∠KAE = ∠CHE ( = 900 )
AE = HE ( ΔBAE = ΔBHE (cmt)
∠AEK = ∠HEC ( 2 góc đối đỉnh )
=> ΔKAE = ΔCHE ( g.c.g )
=> EK = EC ( 2 cạnh tương ứng )

a: Xét ΔABE vuông tại A và ΔHBE vuông tại H có
BE chung
\(\widehat{ABE}=\widehat{HBE}\)
Do đó: ΔABE=ΔHBE
b: Ta có:ΔABE=ΔHBE
nên BA=BH và EA=EH
=>BE là đường trung trực của AH
c: Xét ΔAEK vuông tại A và ΔHEC vuông tại H có
EA=EH
\(\widehat{AEK}=\widehat{HEC}\)
Do đó: ΔAEK=ΔHEC
Suy ra: EK=EC
hay ΔEKC cân tại E
d: Xét ΔBKC có BA/AK=BH/HC
nên AH//KC

Xét hai tam giác vuông BHA và BAC có:
\(\left\{{}\begin{matrix}\widehat{B}\text{ chung}\\\widehat{BHA}=\widehat{BAC}=90^0\end{matrix}\right.\)
\(\Rightarrow\Delta BHA\sim\Delta BAC\left(g.g\right)\)
Xét ΔBHA và ΔBAC có:
\(\widehat{ABC}chung\)
\(\widehat{BHA}=\widehat{BAC}\left(=90^o\right)\)
⇒ ΔBHA ∾ ΔBAC ( g.g )

A.Xét ΔABE và ΔDBE có:
Cạnh BE chung
BD = BA
⇒ ΔABE = ΔDBE (cạnh huyền – góc nhọn)
b. Do BD = BA nên B nằm trên đường trung trực của AD
Do ΔABE = ΔDBE ⇒ AE = ED (hai cạnh tương ứng)
E nằm trên đường trung trực của AD
Vậy BE là đường trung trực của AD
c. Do ΔABE = ΔDBE ⇒ ∠(ABE) = ∠(EBC) (hai góc tương ứng)
Suy ra BE là tia phân giác của góc ABC

1) Xét ΔHBA vuông tại H và ΔABC vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔHBA\(\sim\)ΔABC(g-g)
Suy ra: \(\dfrac{HB}{AB}=\dfrac{AB}{BC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(AB^2=BH\cdot BC\)
freqché tonery élooin shçç
arzàyu radio rubsz tqsd
çàèé sonuhy,lafneq toin
çàea & reszao and shoppea
reach 123 tusqi yuoyuè
(reachèst)