 giúp câu 30 và 26 thui ạ
giúp câu 30 và 26 thui ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(A=\dfrac{\left(x^2-2x+5\right)\left(x-3\right)}{3\left(x-3\right)}=\dfrac{x^2-2x+5}{3}\)

4:
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
b: AH=căn 9*16=12cm
AC=căn 12^2+16^2=20cm
HK=16*12/20=192/20=9,6cm
5:
a: Xét ΔMNP vuông tại N và ΔMHN vuông tại H có
góc M chung
=>ΔMNP đồng dạng với ΔMHN
b: NH=căn 16*9=12cm
NP=căn 16^2+12^2=20cm
HK=16*12/20=192/20=9,6cm

a: Xét ΔEAB có \(\widehat{EBA}=\widehat{EAB}\)
nên ΔEAB cân tại E
mà EK là đường cao
nen K là trung điểm của AB
hay KA=KB
b: Xét ΔACE vuông tại C và ΔBDE vuông tại D có
EA=EB
\(\widehat{AEC}=\widehat{BED}\)
Do đó: ΔACE=ΔBDE
Suy ra: EC=ED
Ta có: AE+ED=AD
BE+CE=BC
mà AE=BE
và ED=EC
nên AD=BC

Câu 15
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{3}=\dfrac{c}{5}=\dfrac{a-b+c}{2-3+5}=\dfrac{-10.2}{4}=-2.55\)
Do đó: a=-5,1; b=-7,65; c=-12,75

b: Thay x=-1 và y=-3 vào (d1), ta được:
-3=-1+2
=>-3=1(loại)
=>A ko thuộc (d1)
Thay x=-1 và y=1 vào (d1), ta đc:
-1+2=1
=>1=1
=>B thuộc (d1)
c: Tọa độ C là:
x+2=-1/2x+2 và y=x+2
=>x=0 và y=2

1.
a, \(\left(C\right)x^2+y^2-6x-2y+6=0\)
\(\Leftrightarrow\left(C\right)\left(x-3\right)^2+\left(y-1\right)^2=4\)
\(\Rightarrow\) Tâm \(I=\left(3;1\right)\), bán kính \(R=2\)
b, Tiếp tuyến đi qua A có dạng: \(\left(\Delta\right)ax+by-5a-7b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I;\Delta\right)=\dfrac{\left|3a+b-5a-7b\right|}{\sqrt{a^2+b^2}}=2\)
\(\Leftrightarrow\left|a+3b\right|=\sqrt{a^2+b^2}\)
\(\Leftrightarrow6ab+8b^2=0\)
\(\Leftrightarrow2b\left(3a+4b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}b=0\\3a+4b=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\Delta_1:x=5\\\Delta_2:4x-3y+1=0\end{matrix}\right.\)
TH1: \(\Delta_1:x=5\)
Tiếp điểm có tọa độ là nghiệm hệ: \(\left\{{}\begin{matrix}x=5\\x^2+y^2-6x-2y+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y^2-2y+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=1\end{matrix}\right.\Rightarrow\left(5;1\right)\)
TH2: \(\Delta_2:4x-3y+1=0\)
Tiếp điểm có tọa độ là nghiệm hệ: \(\left\{{}\begin{matrix}4x-3y+1=0\\x^2+y^2-6x-2y+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{7}{5}\\y=\dfrac{11}{5}\end{matrix}\right.\Rightarrow\left(\dfrac{7}{5};\dfrac{11}{5}\right)\)
Kết luận: Phương trình tiếp tuyến: \(\left\{{}\begin{matrix}\Delta_1:x=5\\\Delta_2:4x-3y+1=0\end{matrix}\right.\)
Tọa độ tiếp điểm: \(\left\{{}\begin{matrix}\left(5;1\right)\\\left(\dfrac{7}{5};\dfrac{11}{5}\right)\end{matrix}\right.\)

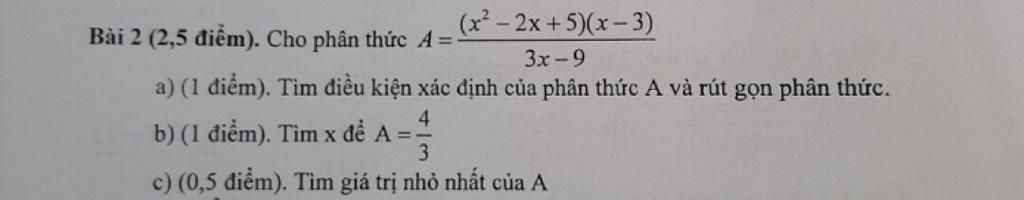


 Giúp em với ăn em cảm ơn mà giúp em mỗi câu 16 thui ạ
Giúp em với ăn em cảm ơn mà giúp em mỗi câu 16 thui ạ các bạn giúp mình câu 5 nhé mình cần gấp lắm ạ!!! chỉ trong tối nay thui ạ !!! cảm ơn
các bạn giúp mình câu 5 nhé mình cần gấp lắm ạ!!! chỉ trong tối nay thui ạ !!! cảm ơn 


Câu 26.
CaO + H2O ---> Ca(OH)2
Ca(OH)2 + Na2CO3 ---> 2NaOH + CaCO3
CaCO3 --to-> CaO + CO2
CaO + 2HCl ---> CaCl2 + H2O
Câu 30.
Khi một vật có khả năng thực hiện công ta nói vật có cơ năng.
VD: Vật đang chuyển động trong không trung, con lắc lò xo dao động.