Cho tam giác ABC, điểm D nằm giữa A và C (BD không vuông góc với AC). Gọi E và F là chân các đường vuông góc kẻ từ A và C đến đường thẳng BD. So sánh AC với tổng AE + CF.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 4 2018
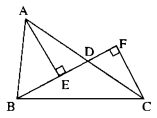
Trong ∆ADE ta có góc AED = 90∘
Nên AE < AD (1)
Trong ∆CFD ta có góc CFD = 90∘
Nên CF < CD (2)
Cộng từng vế (1) và (2) ta có:
AE + CF < AD + CD
Mà D nằm giữa A và C nên AD + CD = AC
Vậy AE + CF < AC
CM
19 tháng 3 2018
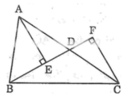
+ AE là đường vuông góc hạ từ đỉnh A xuống đường thẳng BF
⇒ AE < AD. ( quan hệ đường vuông góc và đường xiên). (1)
+ CF là đường vuông góc hạ từ đỉnh C xuống đường thẳng BF
⇒ CF < CD ( quan hệ đường vuông góc và đường xiên). (2)
Từ (1) và (2) vế cộng vế ta được: AE + CF < AD + CD = AC.
8 tháng 5 2020
Trong ∆ADE ta có \(\widehat {A{\rm{ED}}} = 90^\circ \)
Nên AE < AD (1)
Trong ∆CFD ta có \(\widehat {CF{\rm{D}}} = 90^\circ \)
Nên CF < CD (2)
Cộng từng vế (1) và (2) ta có:
AE + CF < AD + CD
Mà D nằm giữa A và C nên AD + CD = AC
Vậy AE + CF < AC
TT
8 tháng 5 2020
Trong ∆ADE ta có góc AED = 90∘
Nên AE < AD (1)
Trong ∆CFD ta có góc CFD = 90∘
Nên CF < CD (2)
Cộng từng vế (1) và (2) ta có:
AE + CF < AD + CD
Mà D nằm giữa A và C nên AD + CD = AC
Vậy AE + CF < AC
LH
Lê Huy Tường
VIP
17 tháng 4 2021
Cho tam giác ABC, điểm D nằm giữa A và C (BD không vuông góc với AC). Gọi E và F là chân các đường vuông góc từ A và C đến BD.
Chọn dấu thích hợp: AC > AE + CF
17 tháng 4 2021
Vì AE⊥BDAE⊥BD nên AE là đường vuông góc hạ từ đỉnh A xuống đường thẳng BD và AD là đường xiên.
Nên AE<ADAE<AD (1) (quan hệ giữa đường xiên và đường vuông góc)
Vì CF⊥BDCF⊥BD nên CF là đường vuông góc hạ từ đỉnh A xuống đường thẳng BD và CD là đường xiên.
Nên CF<CDCF<CD (2) (quan hệ giữa đường xiên và đường vuông góc)
Cộng từng vế (1) và (2) ta có:
AE+CF<AD+CDAE+CF<AD+CD
Mà DD nằm giữa AA và CC nên AD+CD=ACAD+CD=AC
Vậy AE+CF<AC
ΔAED vuông tại E
=>AD là cạnh lớn nhất trong ΔAED
=>AD>AE
Ta có: ΔCFD vuông tại F
=>CD là cạnh lớn nhất trong ΔCFD
=>CD>CF
Ta có: AD>AE
CD>CF
Do đó: AD+CD>AE+CF
=>AC>AE+FC