Chứng minh rằng ko tồn tại số hữu tỉ x và y trái dấu và thỏa mãn đẳng thức 1/x+y=1/x + 1/y
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
LT
4

PT
1

CM
3 tháng 1 2017
Xét số hữu tỉ a/b, có thể coi b > 0.
Nếu a, b khác dấu thì a < 0 và b > 0.
Suy ra (a/b) < (0/b) = 0 tức là a/b âm.
PT
Cho số hữu tỉ a/b khác 0. Chứng minh rằng: a/b là số hữu tỉ dương nếu a và b cùng dấu.
1

CM
22 tháng 8 2017
Xét số hữu tỉ a/b, có thể coi b > 0.
Nếu a, b cùng dấu thì a > 0 và b > 0.
Suy ra (a/b) > (0/b) = 0 tức là a/b dương.

CM
19 tháng 12 2018
Chọn D
Ta có: x(3 + 5i) - y(1 + 2i) = 9 + 16i <=> (3x - y) + (5x - 2y) = 9 + 16i
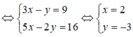
Vậy: T = |x - y| = 5
\(\frac{1}{x+y}=\frac{1}{x}+\frac{1}{y}\Leftrightarrow\frac{1}{x+y}=\frac{x+y}{xy}\Leftrightarrow xy=\left(x+y\right)^2.\)
mà (x + y)2 >=0 với mọi x;y => xy >= 0. => x;y không thể trái dấu. đpcm