Cho x0 là nghiệm của đa thức x2 - 3x+1
Tính:a,x0+1:x0
b,x02+1:x02
c,x03+1:x03
d,x09+1:9
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C.
Điều kiện. x ≠ -1
Phương trình tương đương ![]()
Lấy ln hai vế của , ta được ![]()
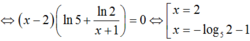
Suy ra x0 = 2 và P = 60.

P(x) = ax0+ b = 0 [Vì x0 là nghiệm của P(x)]
\(\Rightarrow ax_0=-b\Rightarrow b=-ax_0\)
Ta có:\(P\left(x\right)=ax+b\)
\(Thay:b=-ax_0\)
\(\Rightarrow P\left(x\right)=-ax_0+a=a.\left(x-x_0\right)\)
Akai HarumaMashiro ShiinaNguyễn Huy TúngonhuminhĐỗ Thanh Hải
help tui![]()

Dễ thấy: \(x_0;y_0\ne 0\)
*)Xét \(x_0;y_0>0\) xài BĐT AM-GM
\(x^3+y^3+1\ge3\sqrt[3]{x^3y^3}=3xy\)
Xảy ra khi \(x=y=1\)
Khi đó \(\left(1+x_0\right)\left(1+\dfrac{1}{y_0}\right)\left(1+\dfrac{x_0}{y_0}\right)=8\)
*)Xét \(x_0;y_0<0\)\(\Rightarrow3xy>0;x^3+y^3+1\le0\) (loại)

ĐKXĐ: \(m\ne-\dfrac{1}{3}\)
a) Để (P) đi qua điểm \(E\left(\dfrac{1}{2};\dfrac{1}{4}\right)\) thì
Thay \(x=\dfrac{1}{2}\)và \(y=\dfrac{1}{4}\) vào hàm số \(y=\left(3m+1\right)x^2\), ta được:
\(\left(3m+1\right)\cdot\dfrac{1}{4}=\dfrac{1}{4}\)
\(\Leftrightarrow3m+1=1\)
\(\Leftrightarrow3m=0\)
hay m=0(thỏa ĐK)
b) Ta có: \(\left\{{}\begin{matrix}3x-4y=2\\-4x+3y=-5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}12x-16y=8\\-12x+9y=-15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-7y=-7\\3x-4y=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\3x=2+4y=2+4=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy: F(2;1)
Để (P) đi qua điểm F(2;1) thì
Thay x=2 và y=1 vào hàm số \(y=\left(3m+1\right)x^2\), ta được:
\(\left(3m+1\right)\cdot4=1\)
\(\Leftrightarrow3m+1=\dfrac{1}{4}\)
\(\Leftrightarrow3m=-\dfrac{3}{4}\)
\(\Leftrightarrow m=\dfrac{-3}{4}:3=\dfrac{-3}{4}\cdot\dfrac{1}{3}=\dfrac{-1}{4}\)(thỏa ĐK)