Cho hình thang ABCD (AB//CD); AB = 3cm, DC = 6,5cm. Gọi M là giao điểm của DA và CB. a) Chứng minh ∆ MAB ∆ MDC. Tính tỉ số đồng dạng. b) Chứng minh DC.MA = AB.MD. c) Biết diện tích hình thang ABCD bằng 19cm2 , tính khoảng cách giữa hai đáy của hình thang ABCD và diện tích tam giác MAB.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 12 2018
Gợi ý: Kẻ AH ^ CD tại H, kẻ BK ^ CD tại K
Tính được SABCD = 180cm2
1
14 tháng 6 2021
từ A hạ \(AE\perp DC\)
từ B hạ \(BF\perp DC\)
\(AB//CD=>AB//EF\)\(=>ABCD\) là hình chữ nhật
\(=>AB=EF=2cm\)
vì ABCD là hình thang cân\(=>\left\{{}\begin{matrix}AD=BC\\\angle\left(ADE\right)=\angle\left(BCF\right)\end{matrix}\right.\)
mà \(\angle\left(AED\right)=\angle\left(BFC\right)=90^o\)
\(=>\Delta ADE=\Delta BFC\left(ch.cgn\right)=>DE=FC=\dfrac{DC-EF}{2}=\dfrac{6-2}{2}=2cm\)
xét \(\Delta ADE\) vuông tại E có: \(AE=\sqrt{AD^2-ED^2}=\sqrt{3^2-2^2}=\sqrt{5}cm\)
\(=>S\left(ABCD\right)=\dfrac{\left(AB+CD\right)AE}{2}=\dfrac{\left(2+6\right)\sqrt{5}}{2}=4\sqrt{5}cm^2\)
VN
0
CM
21 tháng 6 2018
Đáp án A
Ta có: V = π A H 2 . A B + 1 3 π A H 2 B H + C K = 2 π A H 2 + 2 3 π A H 2
= 6 π ⇔ 2 A H 2 + 2 3 A H 2 = 6 ⇔ A H = 3 2 ⇒ S A B C D = A B + C D 2 . A H = 9 2
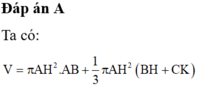
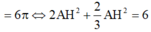
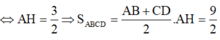
a: Xét ΔMAB và ΔMDC có
\(\widehat{MAB}=\widehat{MDC}\)
\(\widehat{M}\) chung
Do đó: ΔMAB∼ΔMDC
b: Ta có: ΔMAB∼ΔMDC
nên AB/DC=MA/MD
hay \(AB\cdot MD=DC\cdot MA\)