Giải giùm mình với ak
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(S=2S-S\)
\(=2\left(1+\dfrac{1}{2}+...+\dfrac{1}{2^{2022}}\right)-\left(1+\dfrac{1}{2}+...+\dfrac{1}{2^{2022}}\right)\)
\(=\left(2+1+...+\dfrac{1}{2^{2021}}\right)-\left(1+\dfrac{1}{2}+...+\dfrac{1}{2^{2022}}\right)\)
\(=2-\dfrac{1}{2^{2022}}< 2\left(đpcm\right)\)
bài thi tui có bài này (0.5 điểm ) khó quá nên bỏ qua luôn
nói chung ko bt làm

Đổi 5.75 phút= 345 giây= 5 phút 45 giây
Thời gian bạn Hà chạy nhanh hơn bạn Nam là
6 phút 13 giây- 5 phút 45 giây= 28 (giây)



Diện tích hình tam giác BKC là : 15 * 8 : 2 = 60 cm
Diện tích hình tam giác ABC là : 60 * 2 = 120 cm²
Đ/s : 120 cm²
Giải giùm e bài này với ak
Chứng minh rằng nếu cos^2 A +cos ^2 B + cos^2 C = 1 thì tam giác ABC vuông






 Giải giùm mình với~
Giải giùm mình với~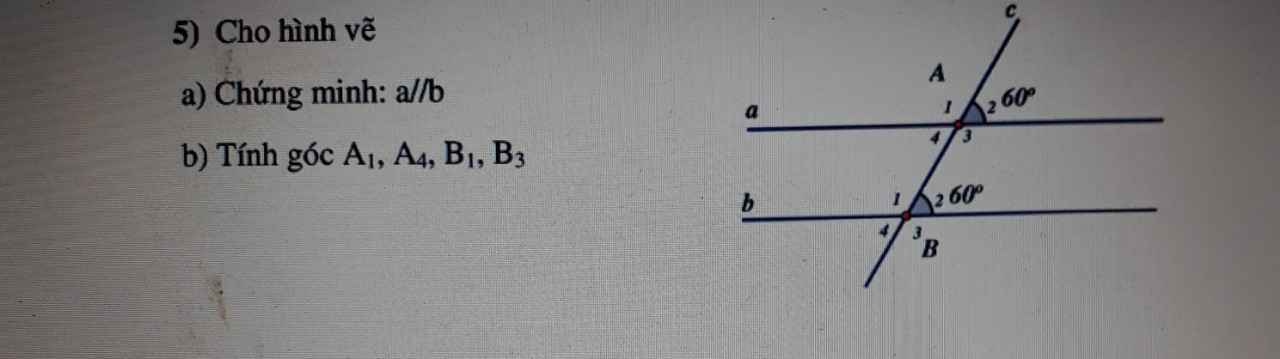
a) Đây là biến thế hạ thế vì nó làm giảm hiệu điện thế
b) Có \(\dfrac{U_1}{U_2}=\dfrac{N_1}{N_2}\Leftrightarrow\dfrac{220}{6}=\dfrac{N_1}{30}\Leftrightarrow N_1=1100\)(vòng)
Bài 2:
Tóm tắt:
AB = 2cm
OA = 30cm
OF = OF' = 20cm
A'B' = ?
OA' = ?
Giải:
\(\Delta ABF\sim\Delta OIF\)
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}=\dfrac{2}{A'B'}=\dfrac{30-20}{20}\)
=> A'B' = 6cm
\(\Delta OAB\sim\Delta OA'B'\)
\(\Rightarrow\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}\Leftrightarrow\dfrac{30}{OA'}=\dfrac{2}{6}\Rightarrow OA'=90cm\)