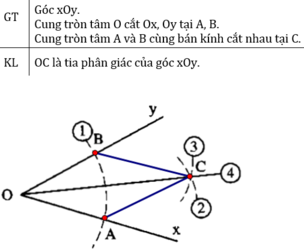
cho góc xoy vẽ cung tròn tâm o cung này cắt ox oy theo thứ tự ở A và B có cùng bán kính sao cho chúng cắt nhau ở điểm C nằm trong góc xoy nối o với C chứng minh oc là tia phân giác góc xoy
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 3 2016
xem hình vẽ:
Nối BC, AC.
∆OBC và ∆OAC có:
OB=OA(Bán kính)
BC=AC(gt)
OC cạnh chung
nên∆OBC = ∆OAC(c.c.c)
Nên BOC=AOC (hai góc tương ứng)
Vậy OC là tia phân giác xOy.
18 tháng 11 2016
Xét tam giác OBC và tam giác OAC có:
OC: cạnh chung
OB = OA (vì cùng nằm trên 1 cung tròn tâm O)
BC = AC (vì cung tròn tâm A = cung tròn tâm B)
Vậy tam giác OBC = tam giác OAC (c.c.c)
=> góc COB = góc COA (2 góc tương ứng)
=> OC là phân giác của góc xOy (đpcm)
24 tháng 11 2017
Xét \(\Delta OAC\) và \(\Delta OBC\) có:
OA=OB (vì cùng nằm trên cung tròn tâm O)
AC=BC (vì C là giao điểm của cung tròn tâm A và cung tròn tâm B)
OC là cạnh chung
\(\Rightarrow\Delta OAC=\Delta OBC\) (c.c.c)
\(\Rightarrow\widehat{AOC}=\widehat{BOC}\) (hai góc tương ứng) (1)
Vì điểm C nằm trong \(\widehat{xOy}\) nên tia OC nằm giữa 2 tia Ox và Oy (2)
Từ (1) và (2) suy ra tia OC là tia phân giác của \(\widehat{xOy}\) (đpcm)
CM
19 tháng 3 2019
Nối BC, AC
ΔOBC và ΔOAC có:
OB = OA (bán kính)
AC = BC (gt)
OC cạnh chung
Nên ΔOBC = ΔOAC (c.c.c)
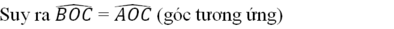
nên OC là tia phân giác của góc xOy.
HH
20 tháng 4 2017
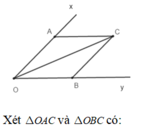
xem hình vẽ:
Nối BC, AC.
∆OBC và ∆OAC có:
OB=OA(Bán kính)
BC=AC(gt)
OC cạnh chung
nên∆OBC = ∆OAC(c.c.c)
Nên ˆBOC=ˆAOCBOC^=AOC^(hai góc tương ứng)
Vậy OC là tia phân giác xOy.
28 tháng 7 2018
vì (o) cắt Õ Oy tại A, B nên OA=OB ( bán kính )
ta có đường tròn tâm A và B có cùng bán kính và cắt nhau tại C nên AC=CB
xét tam giác OAC và tam giác OBC có : OA=OB (cmt) ; AC=CB ( cmt ) ; OC chung => tgiac OAC= tgiac OBC (CCC)
=> góc AOC=góc COB mà OC nằm giữa hai tia Õ và Oy nên OC là pg Oxy
đúng hộ minh
CM
26 tháng 2 2018
Xét và có:
OA = OB (cùng bán kính đường tròn tâm O)
AC = BC (đường tròn tâm A và tâm B cùng bán kính)
OC cạnh chung
Nên OC là tia phân giác của góc xOy => B đúng
+ Tương tự từ (3) suy ra CO là tia phân giác góc ACB.
Vậy cả A, B, C đều đúng.
Chọn đáp án D