ai làm giúp mình bài 4 với 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu trả lời hay nhất: Mùa xuân hoa nở
Tiếng thở thời gian
Ngàn chim vui hót
Thánh thót tiếng đàn
Ngân vang trong gió
Cành lá xanh non
Như bàn tay nhỏ
Gọi gió xuân về
Nắng xuân tràn trề
Lòng người sảng khoái
Tinh thần thoải mái
Làm việc hăng say
Như mùa xuân này
...
Hì hì... Bạn cứ thế mà làm thơ tiếp theo phần còn lại nhé...



Bài 1:
1: \(\left(2a+b\right)^2=4a^2+4ab+b^2\)
2: \(\left(a-3b\right)^2=a^2-6ab+9b^2\)
4: \(\left(3x-5y\right)^2=9x^2-30xy+25y^2\)
7: \(\left(3x-1\right)^2=9x^2-6x+1\)
9: \(\left(x+\dfrac{1}{2}\right)^2=x^2+x+\dfrac{1}{4}\)
10: \(\left(3x-\dfrac{1}{2}\right)^2=9x^2-3x+\dfrac{1}{4}\)
11: \(\left(4-\dfrac{1}{2}x\right)^2=16-4x+\dfrac{1}{4}x^2\)
12: \(\left(3x-0.5\right)^2=9x^2-3x+\dfrac{1}{4}\)
13: \(\left(4x-0.25\right)^2=16x^2-2x+\dfrac{1}{16}\)

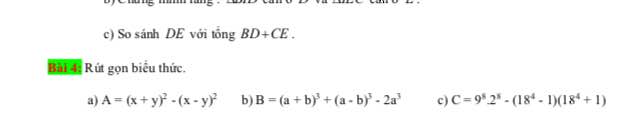


Câu 4:
1. Hiển nhiên $AD\parallel BC$. Áp dụng định lý Talet:
$\frac{BM}{AN}=\frac{PM}{PN}$
$\frac{CM}{NE}=\frac{PM}{PN}$
$\Rightarrow \frac{BM}{AN}=\frac{CM}{NE}$. Mà $BM=CM$ do $M$ là trung điểm $BC$ nên $AN=NE$. $N$ thì nằm giữa $A,E$ (dễ cm)
Do đó $N$ là trung điểm $AE$
2.
Xét tam giác $ABC$ và $DCA$ có:
$\widehat{ABC}=\widehat{DCA}=90^0$
$\widehat{BCA}=\widehat{CAD}$ (so le trong)
$\Rightarrow \triangle ABC\sim \triangle DCA$ (g.g)
3. Theo định lý Pitago:
Từ tam giác đồng dạng phần 2 suy ra:
$\frac{AC}{DA}=\frac{BC}{CA}$
$\Rightarrow AD=\frac{AC^2}{BC}=\frac{6^2}{4}=9$ (cm)
4,Theo phần 1 thì:
$\frac{PM}{PN}=\frac{BM}{AN}=\frac{CM}{AN}$
Mà cũng theo định lý Talet: $\frac{CM}{AN}=\frac{QM}{QN}$
$\Rightarrow \frac{PM}{PN}=\frac{QM}{QN}$
(đpcm)
Hình vẽ:
