Cho một thấu kính hội tụ có tiêu cự 8cm . Đặt một vật sáng AB cao 1cm vuống góc với trục chính của thấy kính (A nằm trên trục chính)
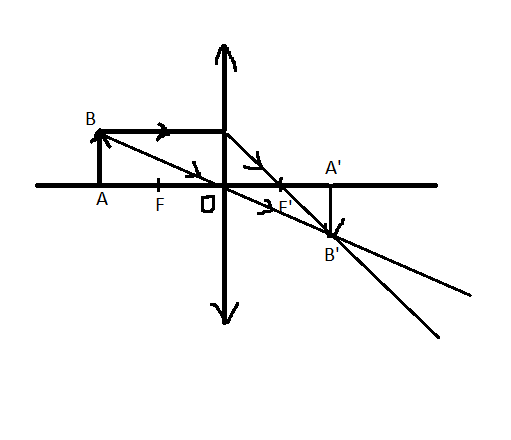
a) Khi vật sáng AB cách thấu kính 15cm. Hãy dựng ảnh củavaatj Ab qua thấu kính hội tụ
b) Nhận xét đặc đieemr của ảnh A'B' của AB
c) Tính khoảng cách từ ảnh đến thấu kính và chiều cao ảnh
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

-Vẽ trục chính.
-Dựng quang tâm O.
-Dựng OF=5cm, OA=15cm.Lấy F' đối xứng với F qua O.
-Từ A vẽ ảnh AB thẳng đứng, vuông góc với trục chính.
-Nối B với O.
-Qua B kẻ đường thẳng song song với trục chính và đi qua F'.
-Hai đường thẳng trên cắt nhau tại đâu là điểm B'. Từ B' dựng vuông góc với trục chính đc ảnh A'B'.

b) ảnh A'B' là ảnh ảo ngược chiều và nhỏ hơn vật
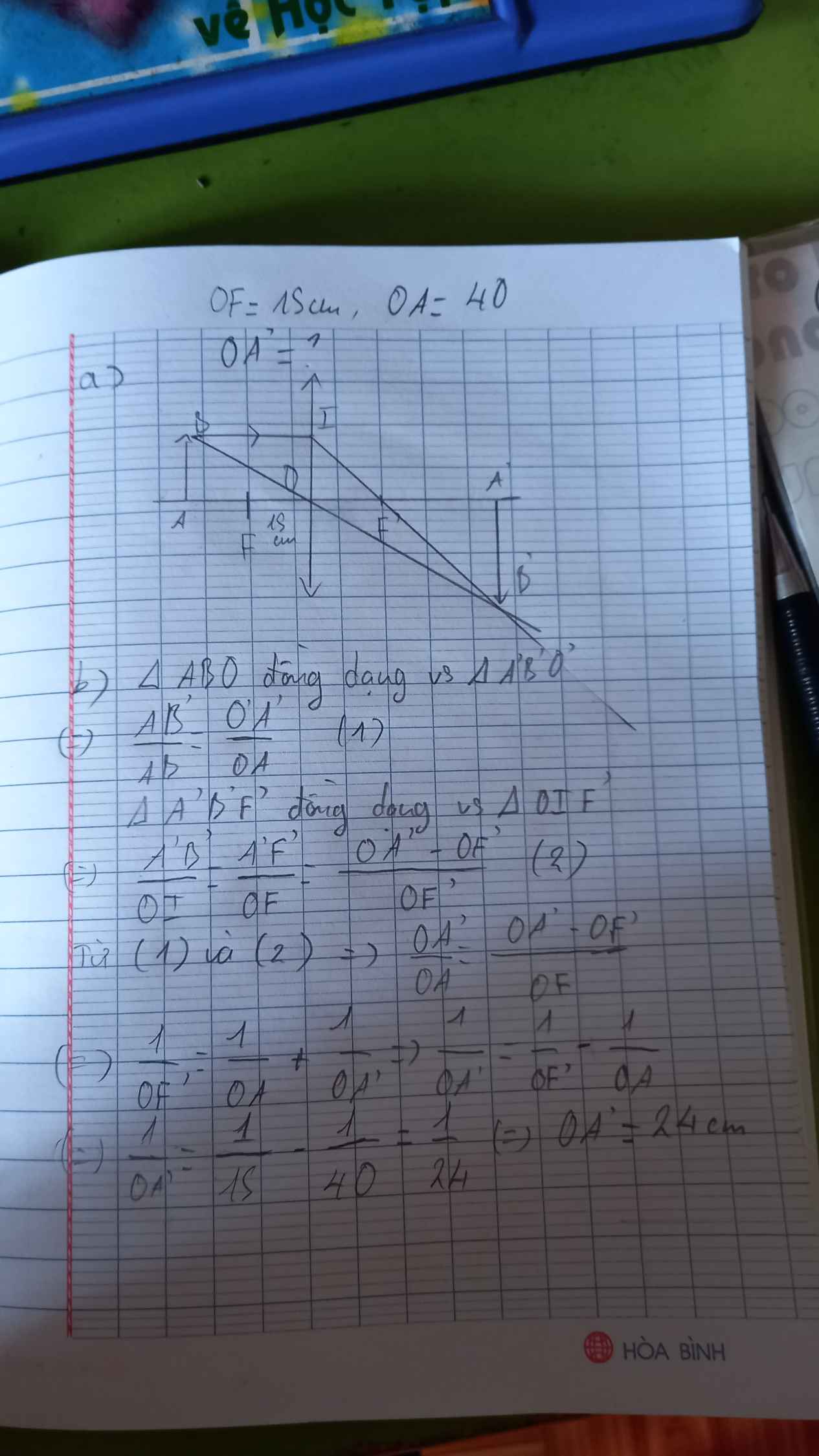
c) ΔOAB∞ΔOA'B'
⇒\(\dfrac{AB}{A'B'}=\dfrac{OA}{OA'}\Rightarrow\dfrac{1}{A'B'}=\dfrac{5}{OA'}\) 1
ΔOFI∞ΔFA'B'
\(\dfrac{OI}{A'B'}=\dfrac{OF'}{F'A'}\Rightarrow\dfrac{AB}{A'B'}\dfrac{OF}{OF-OA}\)
\(\Leftrightarrow\dfrac{1}{A'B'}=\dfrac{3}{3-OA'}\) 2
Từ 1 và 2 ⇒ \(\dfrac{1}{OA'}=\dfrac{3}{3-OA'}\)
⇔1(3-OA') = 3. OA'
⇔3- 3.OA' = 3.OA'
⇔-3.OA' -3. OA' = -3
⇔-6.OA' = -3
⇔OA' = -9
Thay OA'= -9 vào 1
⇒\(\dfrac{1}{A'B'}=\dfrac{5}{-9}\Rightarrow A'B'=\dfrac{1.\left(-9\right)}{5}=-1.8\)

Khoảng cách từ ảnh đến thấu kính là:
Áp dụng công thức tính thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{d.f}{d-f}=\dfrac{8.4}{8-4}=8\left(cm\right)\)
Chiều cao của ảnh:
Ta có: \(\dfrac{d}{d'}=\dfrac{h}{h'}\Rightarrow h'=\dfrac{d'.h}{d}=\dfrac{8.2}{8}=2\left(cm\right)\)

Ảnh cao bằng nửa vật\(\Rightarrow h'=\dfrac{1}{2}h\)
\(\Rightarrow\dfrac{h}{h'}=\dfrac{1}{2}\)
Mà \(\dfrac{d}{d'}=\dfrac{h}{h'}=\dfrac{1}{2}\Rightarrow d'=2d=2\cdot15=30cm\)
Tiêu cự thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{15}+\dfrac{1}{30}=\dfrac{1}{10}\)
\(\Rightarrow f=10cm\)

Ảnh thật, ngược chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{8}=\dfrac{1}{12}+\dfrac{1}{d'}\)
\(\Rightarrow d'=24cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{2}{h'}=\dfrac{12}{24}\Rightarrow h'=4cm\)

Ảnh thật, ngược chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{10}=\dfrac{1}{15}+\dfrac{1}{d'}\Rightarrow d'=30cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{1}{h'}=\dfrac{15}{30}\Rightarrow h'=2cm\)
Ảnh ảo, ngược chiều và nhỏ hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{8}=\dfrac{1}{15}+\dfrac{1}{d'}\Rightarrow d'=\dfrac{120}{7}cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{1}{h'}=\dfrac{15}{\dfrac{120}{7}}\Rightarrow h'=\dfrac{8}{7}cm\approx1,14cm\)