mong mọi người giúp dỡ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
7
19 tháng 11 2023
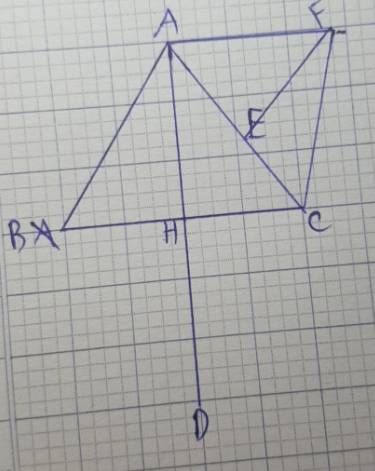
a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)
AH
Akai Haruma
Giáo viên
6 tháng 9 2021
Bài 2:
a.
$P=M+N=-xy^2+3x^2y-x^2y^2+\frac{1}{2}x^2y-xy^2+\frac{-2}{3}x^2y^2$
$=(-xy^2-xy^2)+(3x^2y+\frac{1}{2}x^2y)+(-x^2y^2+\frac{-2}{3}x^2y^2)$
$=-2xy^2+\frac{7}{2}x^2y-\frac{5}{3}x^2y^2$
b.
$Q=N-M=(\frac{1}{2}x^2y-xy^2+\frac{-2}{3}x^2y^2)-(-xy^2+3x^2y-x^2y^2)$
$=(\frac{1}{2}x^2y-3x^2y)-xy^2+xy^2+(\frac{-2}{3}x^2y^2+x^2y^2)$
$=\frac{-5}{2}x^2y+\frac{1}{3}x^2y^2$
c.
$Q=\frac{-5}{2}(-1)^2.\frac{1}{2}+\frac{1}{3}(-1)^2.(\frac{1}{2})^2=\frac{-7}{6}$
AH
Akai Haruma
Giáo viên
6 tháng 9 2021
Bài 3:
a.
$A(x)=\frac{1}{3}x^2-2x^3+2x-\frac{4}{3}x^2-x-1$
$=-2x^3-x^2+x-1$
$A(x)$ có hệ số cao nhất là $-2$ và hệ số tự do là $-1$
$B(x)=2x^3+x^2+1$
$B(x)$ có hệ số cao nhất là $2$ và hệ số tự do là $1$
b.
$B(x)=(2x^3+2x^2)-(x^2-1)=2x^2(x+1)-(x-1)(x+1)$
$=(x+1)(2x^2-x+1)$
$B(-1)=(-1+1)(2x^2-x+1)=0$ nên $-1$ là nghiệm của $B(x)$
c.
$C(x)=A(x)+B(x)=-2x^3-x^2+x-1+(2x^3+x^2+1)$
$=x$
d.
$C(x)=0\Leftrightarrow x=0$
Vậy $x=0$ là nghiệm của $C(x)$
30 tháng 12 2021
a: Xét tứ giác OAMD có
OA//MD
OD//AM
Do đó: OAMD là hình bình hành
mà \(\widehat{AOD}=90^0\)
nên OAMD là hình chữ nhật
TG
2 tháng 6 2021
a)
\(\left(x+1\right)\left(x-3\right)\left(x^2-2x\right)=-2\)
<=> (x + 1).(x - 3).x.(x - 2) = -2
<=> [ (x + 1). (x - 3) ]. [ x. (x - 2) ] = -2
\(\Leftrightarrow\left(x^2-2x-3\right).\left(x^2-2x\right)+2=0\) (1)
Đặt \(x^2-2x=a\)
PT (1) <=> (a - 3).a + 2 = 0
\(\Leftrightarrow a^2-3a+2=0\)
\(\Leftrightarrow a^2-a-2a+2=0\)
<=> a. (a - 1) - 2. (a - 1) = 0
<=> (a - 1). (a - 2) = 0
<=> a - 1 = 0 hoặc a - 2 = 0
\(\Leftrightarrow\left[{}\begin{matrix}x^2-2x-1=0\\x^2-2x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-1\right)^2-2=0\\\left(x-1\right)^2-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x-1-\sqrt{2}\right).\left(x-1+\sqrt{2}\right)=0\\\left(x-1-\sqrt{3}\right).\left(x-1+\sqrt{3}\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1+\sqrt{2}\\x=1-\sqrt{2}\\x=1+\sqrt{3}\\x=1-\sqrt{3}\end{matrix}\right.\)
2 tháng 6 2021
b) \(\left\{{}\begin{matrix}x^2+x-y^2-y=0\left(1\right)\\x^2+y^2-2\left(x+y\right)=0\left(2\right)\end{matrix}\right.\)
PT (1)\(\Leftrightarrow\left(x-y\right)\left(x+y\right)+\left(x-y\right)=0\)
\(\Leftrightarrow\left(x-y\right)\left(x+y+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=y\\x+y=-1\end{matrix}\right.\)
TH1: x=y thay vào Pt (2) ta được: \(2x^2-4x=0\Leftrightarrow\left[{}\begin{matrix}x=0\Rightarrow y=0\\x=2\Rightarrow y=2\end{matrix}\right.\)
TH2: Thay x+y=-1 vào Pt (2) ta được: \(x^2+y^2+2=0\left(vn\right)\)
Vậy hẹ pt có nghiệm (x;y)=(0;0) ; (2;2)
Mong mọi người giúp đỡ =(
KY
24 tháng 9 2021
more beautiful->the most beautiful
hotter->the hottest
crazier=>the craziest
slowliest->the slowliest
fewer->the fewest
less->the least
worse->the worst
better=>the best
more attractive=>the most attractive
bigger=>the biggest
24 tháng 9 2021
so sánh hơn so sánh nhất
1. more beautiful the most beautiful
2. hotter the hottest
3. crazier the craziest
4. more slowly the most slowly
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 1 2022
Gọi số CLB tối đa là x (nguyên dương).
Theo nguyên lý Dirichlet, từ 10 học sinh nào đó luôn có ít nhất \(\left[\dfrac{10+x-1}{x}\right]\) học sinh tham gia cùng 1 CLB
\(\Rightarrow\left[\dfrac{9+x}{x}\right]=3\Rightarrow\left[\dfrac{9}{x}+1\right]=3\)
\(\Rightarrow\left[\dfrac{9}{x}\right]+1=3\Rightarrow\left[\dfrac{9}{x}\right]=2\)
\(\Rightarrow2\le\dfrac{9}{x}< 3\Rightarrow3< x\le\dfrac{9}{2}\)
\(\Rightarrow x=4\)
Khi đó theo nguyên lý Dirichlet luôn tồn tại 1 CLB có ít nhất \(\left[\dfrac{35+4-1}{4}\right]=9\) học sinh
uk, mk sẽ giúp đỡ bn bằng cách báo cáo bn
một vé báo cáo rất to và vàng: