Cho tứ giác ABCD nội tiếp đường tròn O bán kính R, AC vuông góc BD. Chứng minh AB2+ CD2 không đổi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


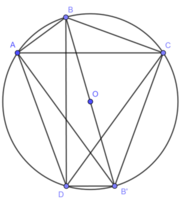
Kẻ đường kính BB’. Nối B’A, B’D, B’C.
Ta có: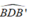 = 90° ( góc nội tiếp chắn nửa đường tròn)
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ AC // B'D ( cùng vuông góc với BD)
Suy ra, tứ giác ADB’C là hình thang
Vì ADB’C nội tiếp đường tròn (O) nên ADB’C là hình thang cân
⇒ CD = AB'
⇒ A B 2 + C D 2 = A B 2 + A B ' 2
Mà tam giác BAB’ vuông tại A do 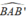 = 90° ( góc nội tiếp chắn nửa đường tròn)
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ A B 2 + C D 2 = A B 2 + A B ' 2 = 2 R 2 = 4 R 2 (đpcm)


a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
A B C D E O
Gọi DE là đường kính của (O;R)
Dễ thấy \(\hept{\begin{cases}AC\perp BD\\BE\perp BD\end{cases}}\)\(\Rightarrow BE\text{//}AC\Rightarrow BECA\)là hình thang mà BECA nội tiếp (O;R) nên BECA là hình thang cân.
Do đó ta có : AB = CE \(\Rightarrow AB^2+CD^2=CE^2+CD^2=DE^2=\left(2R\right)^2=4R^2\) không đổi.
Vậy ta có điều phải chứng minh.