cho tam giác abc các tia phân giác của các góc B và C cắt nhau ở i .qua i kẻ đường thẳng song song với BC cắt các cạnh AB và AC ở D và E
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
9 tháng 3 2019
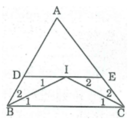
Đường thẳng đi qua I song song với BC cắt AB tại D và AC tại E, ta có các hình thang sau: BDEC, BDIC, BIEC
CM
19 tháng 1 2017
DE // BC (theo cách vẽ)
⇒ ∠ I 1 = ∠ B 1 (hai góc so le trong)
Mà ∠ B 1 = ∠ B 2 (gt)
Suy ra: ∠ I 1 = ∠ B 2
Do đó: ∆ BDI cân tại D ⇒ DI = DB (1)
Ta có: ∠ I 2 = ∠ C 1 (so le trong)
∠ C 1 = ∠ C 2 (gt)
Suy ra: ∠ I 2 = ∠ C 2 do đó: ∆ CEI cân tại E
⇒ IE = EC (2)
DE = DI + IE (3)
Từ (1), (2), (3) suy ra: DE = BD + CE
5 tháng 2 2017
\(\widehat{I_1}=\widehat{B_2}\)(2 góc slt của DE // BC) mà\(\widehat{B_1}=\widehat{B_2}\)(BI là phân giác góc ABC)\(\Rightarrow\widehat{I_1}=\widehat{B_1}\Rightarrow\Delta BDI\)cân tại D => BD = DI
\(\widehat{I_2}=\widehat{C_2}\)(2 góc slt của DE // BC) mà\(\widehat{C_1}=\widehat{C_2}\)(CI là phân giác góc ACB)\(\Rightarrow\widehat{I_2}=\widehat{C_1}\Rightarrow\Delta IEC\)cân tại E => IE = EC
Vậy DE = DI + IE = BD + CE (đpcm)
6 tháng 2 2017
Vì DE song song với BC => \(\widehat{DIB}=\widehat{IBC}\) ( SLT) . Mà \(\widehat{IBC}=\widehat{DBI}\) ( BI là p/g của \(\widehat{ABC}\) ) => \(\widehat{DIB}=\widehat{DBI}\) theo định lý => tam giác DIB cân tại D => DB = DI
Vì DE song song với BC => \(\widehat{EIC}=\widehat{ICB}\)( SLT) .Mà \(\widehat{ECI}=\widehat{ICB}\) ( CI là p/g của \(\widehat{ECB}\) ) => \(\widehat{EIC}=\widehat{ECI}\) .Theo định lý => tam giác IEC cân tại E => EI = EC
Vì DE = DI + IE . Mà DI = DB ; IE = EC => DE = DB + CE
Vậy DE = DB + CE
CM
22 tháng 4 2018
Đáp án cần chọn là: D
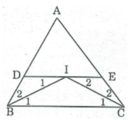
Xét tứ giác DECB có: DE // BC (gt) nên tứ giác DECB là hình thang.
Tương tự:
Tứ giác DICB có DI // BC (gt) nên tứ giác DICB là hình thang.
Tứ giác IECB có IE // CB (gt) nên tứ giác IECB là hình thang.
CM
22 tháng 3 2017
Đáp án cần chọn là: B
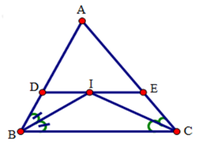
Vì DE // BC (gt) nên suy ra D I B ^ = I B C ^ (so le trong)
Mà D I B ^ = I B C ^ (gt) nên D I B ^ = D B I ^
Suy ra tam giác BDI cân đỉnh D.
Do đó DI = DB (1)
Ta có: IE // CB nên suy ra E I C ^ = B C I ^ (so le trong)
Mà E I C ^ = B C I ^ (gt) nên E C I ^ = E I C ^
Suy ra tam giác EIC cân đỉnh E
Do đó EI = EC (2)
Cộng (1) và (2) vế theo vế ta được: DI + EI = BD + CE
=> DE = BD + CE
CM
26 tháng 5 2019
Đáp án cần chọn là: D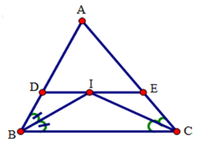
Xét tứ giác DECB có: DE // BC (gt) nên tứ giác DECB là hình thang.
Tương tự:
Tứ giác DICB có DI // BC (gt) nên tứ giác DICB là hình thang.
Tứ giác IECB có IE // CB (gt) nên tứ giác IECB là hình thang.
CM
9 tháng 1 2018
Đáp án cần chọn là: B
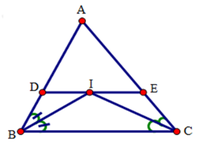
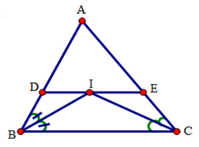
Vì DE // BC (gt) nên suy ra D I B ^ = I B C ^ (so le trong)
Mà D B I ^ = I B C ^ (gt) nên D I B ^ = D B I ^
Suy ra tam giác BDI cân đỉnh D.
Do đó DI = DB (1)
Ta có: IE // CB nên suy ra E I C ^ = B C I ^ (so le trong)
Mà B C I ^ = E C I ^ (gt) nên E C I ^ = E I C ^
Suy ra tam giác EIC cân đỉnh E
Do đó EI = EC (2)
Cộng (1) và (2) vế theo vế ta được: DI + EI = BD + CE
=> DE = BD + CE