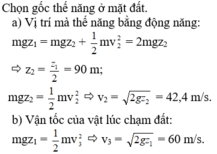Một vật rơi không vận tốc đầu từ độ cao 20m xuống đất. Lấy g = 10m/s2. Bỏ qua mọi lực cản.
a) Xác định vận tốc mà tại đó động năng bằng 1/3
thế năng.
b) Xác định độ cao tại đó động năng bằng 1/4
cơ năng.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
C
☆Châuuu~~~(๑╹ω╹๑ )☆
12 tháng 3 2022
Đúng(2)
Những câu hỏi liên quan
2
6 tháng 5 2022
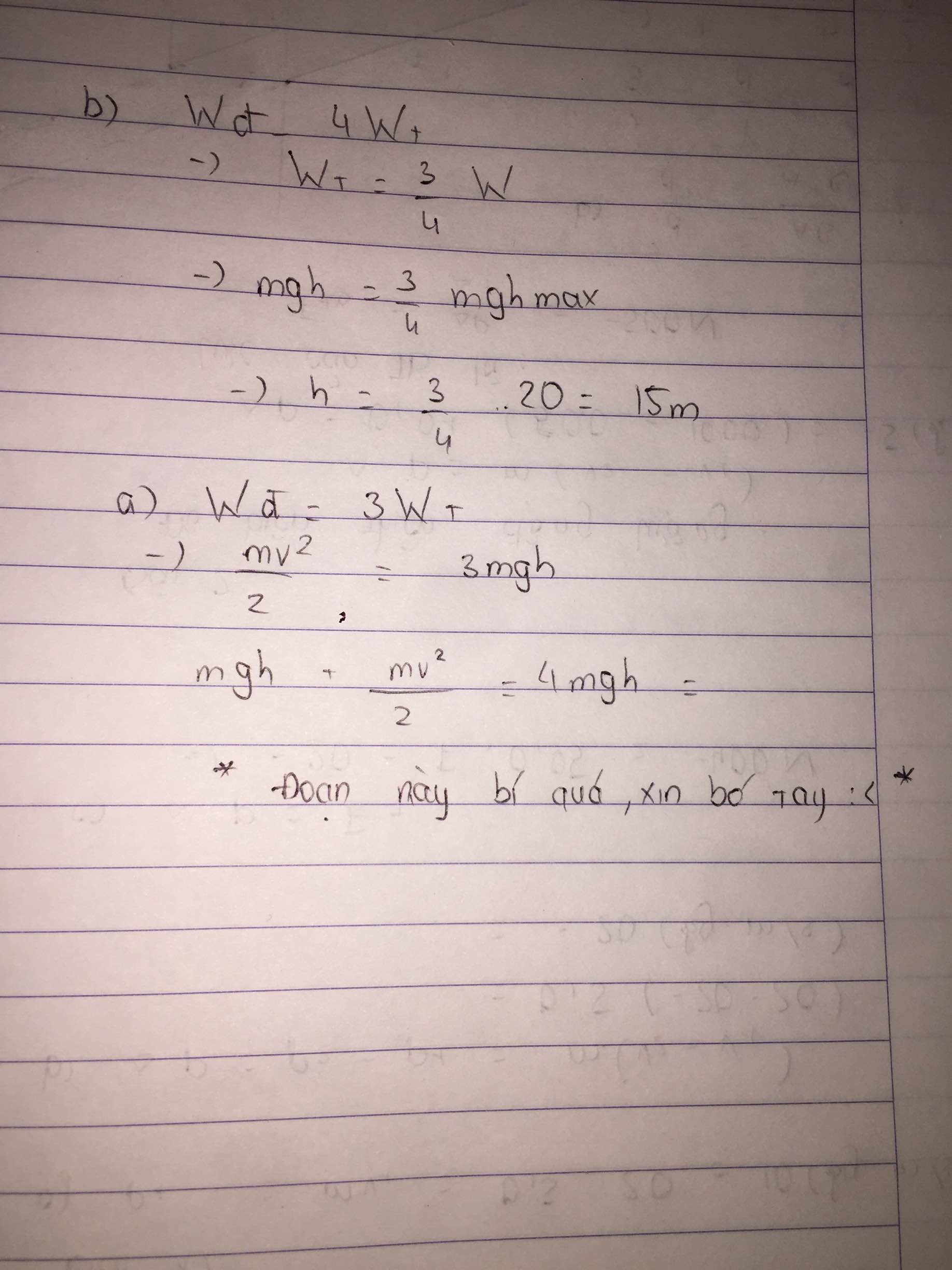
Chọn mốc thế năng tại mặt đất
`a)W_[20 m]=W_[t(20m)]+W_[đ(20m)]=mgz_[20m] + 1/2mv_[20m]^2`
`=m.10.20+1/2 . m . 15^2=312,5m (J)`
`b)W=W_t+W_đ` mà `W_đ=W_t`
`=>W=2W_t`
`=>312,5m = 2 mgz = 2m.10.z`
`=>z=15,625(m)`
`c)W_[đ(max)]=W=312,5m`
`<=>1/2mv_[max]^2=312,5m`
`<=>v_[max]=25 (m//s)`
23 tháng 3 2022
Vận tốc đầu: \(v=0\)m/s
Cơ năng ban đầu:
\(W=\dfrac{1}{2}mv^2+mgz=0,05\cdot10\cdot60=30J\)
Chọn gốc thế năng tại mặt đất.
Cơ năng tại nơi cách đất 20m là:
\(W'=\dfrac{1}{2}mv'^2+mgz'=\dfrac{1}{2}\cdot0,05\cdot v'^2+0,05\cdot10\cdot20\)
Bảo toàn cơ năng: \(W=W'\)
\(\Rightarrow30=\dfrac{1}{2}\cdot0,05\cdot v'^2+0,05\cdot10\cdot20\)
\(\Rightarrow v'^2=800\Rightarrow v'=20\sqrt{2}\)m/s
VT
29 tháng 4 2019
a. Chọn mốc thế năng tại mặt đất
Theo định luật bảo toàn cơ năng ta có
Vậy vận tốc của vật tại vị trí bất kỳ không phụ thuộc vào khối lượng của nó.
b. Gọi B là độ cao cực đại mà vật có thể lên tới. Theo định luật bảo toàn cơ năng
W A = W B ⇒ 1 2 m v A 2 + m g z A = m g z B ⇒ 1 2 .10 2 + 10.15 = 10. z B ⇒ z B = 20 ( m )
c. Gọi C là vị trí W d = 3 W t . Theo định luật bảo toàn cơ năng
W A = W C ⇒ 1 2 m v A 2 + m g z A = W dD + W t = 4 3 W dD ⇒ 1 2 m v A 2 + m g z A = 4 3 . 1 2 m v C 2 ⇒ 1 2 .10 2 + 10.15 = 4 6 v C 2 ⇒ v C = 10 3 ( m / s )
Mà W d = 3 W t ⇒ 1 2 m v 2 = 3 m g z ⇒ z = v 2 6 g = ( 10 3 ) 2 6.10 = 5 ( m )
d.Theo định luật bảo toàn năng lượng
1 2 m v M D 2 = − m g s + A C ⇒ 1 2 m v M D 2 = − m g s + F C . s ⇒ F C = m v M D 2 2 s + m g
Theo định luật bảo toàn cơ năng
W A = W M D ⇒ 1 2 m v A 2 + m g z A = 1 2 m v M D 2 ⇒ v M D = v A 2 + 2 g z A ⇒ v M D = 10 2 + 2.10.15 = 20 ( m / s )
Vậy lực cản của đất
F C = 1.20 2 2.0 , 8 + 1.10 = 260 ( N )
5 tháng 4 2021
Hình bạn tự vẽ nè :^)
Chọn mốc thế năng tại mặt đất ta có
\(W_đ=\dfrac{1}{2}mv^2=\dfrac{1}{2}.0,4.20^2=80\left(J\right)\)
\(W_t=mgh=160\left(J\right)\)
\(W=W_t+W_đ=80+160=240\left(J\right)\)
b) Gọi B là vị trí có độ cao \(H_{max}\)
Ta có: \(W_A=W_B\)
\(\Leftrightarrow\dfrac{1}{2}mv^2+mgh=mgh_{max}\)
\(\Leftrightarrow240=0,4.10.h_{max}\)
\(\Leftrightarrow h_{max}=60\left(m\right)\)
Thời gian chuyển động:
\(h=v_ot+\dfrac{gt^2}{2}\)
\(\Leftrightarrow60=20t+5t^2\)
\(\Leftrightarrow\left[{}\begin{matrix}t=-6\left(Loại\right)\\\\t=2\left(TM\right)\end{matrix}\right.\)
Vậy t=2(s)
Gọi vị trí mà cơ năng bằng 2 thế năng là C
\(\Rightarrow W_C=3W_{tC}\)
áp dụng định luật bảo toàn cơ năng tại A và C:
\(W_A=W_C\)
\(\Leftrightarrow240=2mgh'\)
\(\Leftrightarrow240=2.0,4.10.h'\)
\(\Leftrightarrow h=30\left(m\right)\)
Vậy vị trí cơ năng bằng 2 thế năng có độ cao h=30(m)
HQ
15 tháng 2 2021
a) Chọn trục Ox hướng thẳng đứng lên trên, gốc O tại điểm ném, gốc thời gian t=0
tại thời điểm ném thì:\(\left\{{}\begin{matrix}v=v_0-gt\\x=v_0t-\dfrac{1}{2}gt^2\left(1\right)\end{matrix}\right.\)
Tại điểm cao nhất của vật thì v=0\(\Rightarrow v_0-gt=0\Rightarrow t=\dfrac{v_0}{g}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow x=v_0.\dfrac{v_0}{g}-\dfrac{1}{2}g\left(\dfrac{v_0}{g}\right)^2=\dfrac{v_0^2}{g}=h_{max}\) ( Học thuộc luôn càng tốt :D không phải nhớ cách chứng minh làm gì này viết cho bn hiểu thôi. )
\(\Rightarrow h_{max}=\dfrac{v_0^2}{2g}=5\left(m\right)\)
b) Hình như mình đã chứng minh tổng quát 1 câu hỏi của bạn :D xin phép không chứng minh lại ^^
Bảo toàn cơ năng:
\(W_O=W_A\) \(\Leftrightarrow\dfrac{1}{2}mv^2=4mgh'\) ( lý do tại sao bạn xem lại cách chứng minh :D )
\(\Leftrightarrow h'=1,25\left(m\right)\)
c) \(W=W_đ+W_t=mgz=75\left(J\right)\) ( Tại điểm cao nhất v=0 )