Chứng minh rằng \(\frac{87}{89}<\frac{1}{2\sqrt{1}}+\frac{1}{3\sqrt{2}}+....+\frac{1}{2011\sqrt{2010}}<\frac{88}{45}\)
Ai biết gì giúp mình bài này hơi khó chút
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có 23 chia 7 dư 1 => những số có mũ chia hết cho 3 đều chia 7 dư 1
<=> 23 + 26 + ...+ 290 chia 7 dư 2 ( từ 3 đến 90 có 30 số chia hết cho 3 )
Dãy số còn lại 2, 22, 24,... 289
Đặt A = 2 + 22 +...+289 = (2 + 22) + 23(2 + 22) + ... + 287(2 + 22)
<=> A = (2 + 22)(1 + 23 + ... + 287)
Tương tự ta có từ 3 đến 87 có 29 số chia hết cho 3 => 23 + ... + 287 chia 7 dư 1
=> 1 + 23 + ... + 287 chia 7 dư 2 => A chia 7 dư - 2 ( vì 2 + 22 chia 7 dư -1 )
Vậy T chia hết cho 7

\(\frac{87}{89}< \frac{1}{2}+\frac{1}{3\sqrt{2}}+...+\frac{1}{2011\sqrt{2010}}< \frac{88}{45}\)
Đặt \(A=\frac{1}{2}+\frac{1}{3\sqrt{2}}+...+\frac{1}{2011\sqrt{2010}}\)
\(\frac{1}{\sqrt{k}}-\frac{1}{\sqrt{k+1}}=\frac{1}{\sqrt{k\left(k+1\right)}}>\frac{1}{\left(k+1\right)\sqrt{k}}>\frac{1}{\left(k+1\right)k}=\frac{1}{k}-\frac{1}{k+1}\)
\(\Rightarrow1-\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}-\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{2010}}-\frac{1}{\sqrt{2011}}>A>1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2010}-\frac{1}{2011}\)
\(\Rightarrow1-\frac{1}{\sqrt{2011}}>A>1-\frac{1}{2011}\)
\(\Rightarrow\frac{88}{45}>\frac{2011-\sqrt{2011}}{2011}>A>\frac{2010}{2011}>\frac{87}{89}\)
\(\Rightarrow\frac{87}{89}< \frac{1}{2}+\frac{1}{3\sqrt{2}}+...+\frac{1}{2011\sqrt{2010}}< \frac{88}{45}\)

Ta có: OA = OC (bán kính) nên ΔOAC cân tại O.
suy ra C ^ = O A C ^ 1
Lại có O'A = O'D (bán kính) nên ΔO'AD cân tại O'
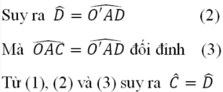
Vậy OC // O'D (có hai góc so le trong bằng nhau).

Ta có: OA = OC (bán kính) nên ΔOAC cân tại O.
![]()
Lại có O'A = O'D (bán kính) nên ΔO'AD cân tại O'

Vậy OC // O'D (có hai góc so le trong bằng nhau).

b) \(\frac{x-11}{89}+\frac{x-13}{87}+\frac{x-15}{85}+\frac{x-17}{83}=4\)
\(=>\left(\frac{x-11}{89}-1\right)+\left(\frac{x-13}{87}-1\right)+\left(\frac{x-15}{85}-1\right)+\left(\frac{x-17}{83}-1\right)=0\)
\(=>\frac{x-100}{89}+\frac{x-100}{87}+\frac{x-100}{85}+\frac{x-100}{83}=0\)
\(=>\left(x-100\right)\left(\frac{1}{89}+\frac{1}{87}+\frac{1}{85}+\frac{1}{83}\right)=0\)
=> x-100 =0 => x=100
Vậy nghiệm là 100

Ta có: 87 - 218 = (23)7 - 218 = 221 – 218 = 217.( 24 -2)= 217.(16 - 2) = 24.14 ⋮ 14

\(A=2^{21}-2^{18}=2^{18}\left(2^3-1\right)=7\cdot2^{18}=14\cdot2^{17}⋮14\\ B=3^{100}-2^{100}+3^{98}-2^{98}\\ B=3^{98}\left(3^2+1\right)-2^{97}\left(2^3+2\right)\\ B=3^{98}\cdot10-2^{97}\cdot10=10\left(3^{98}-2^{97}\right)⋮10\\ C=1+3+3^2+...+3^{99}\\ C=\left(1+3+3^2+3^3\right)+\left(3^4+3^5+3^6+3^7\right)+...+\left(3^{96}+3^{97}+3^{98}+3^{99}\right)\\ C=\left(1+3+3^2+3^3\right)+3^4\left(1+3+3^2+3^3\right)+...+3^{96}\left(1+3+3^2+3^3\right)\\ C=\left(1+3+3^2+3^3\right)\left(1+3^4+...+3^{96}\right)\\ C=40\left(1+3^4+...+3^{36}\right)⋮40\)

\(A=\dfrac{1}{5\times7}+\dfrac{1}{7\times9}+\dfrac{1}{9\times11}+...+\dfrac{1}{87\times89}\)
\(A=\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+...+\dfrac{1}{87}-\dfrac{1}{89}\)
\(A=\dfrac{1}{5}-\left(\dfrac{1}{7}-\dfrac{1}{7}\right)-\left(\dfrac{1}{9}-\dfrac{1}{9}\right)-...-\left(\dfrac{1}{87}-\dfrac{1}{87}\right)-\dfrac{1}{89}\)
\(A=\dfrac{1}{5}-\dfrac{1}{89}\)
\(A=\dfrac{84}{445}\)
Vậy, `A=84/445.`
A = \(\dfrac{1}{5\times7}\) + \(\dfrac{1}{7\times9}\)+\(\dfrac{1}{9\times11}\)+...+\(\dfrac{1}{87\times89}\)
A = \(\dfrac{1}{2}\) \(\times\)( \(\dfrac{2}{5\times7}\)+\(\dfrac{2}{7\times9}\)+\(\dfrac{2}{9\times11}\)+...+\(\dfrac{2}{87\times89}\))
A = \(\dfrac{1}{2}\) \(\times\) ( \(\dfrac{1}{5}\) - \(\dfrac{1}{7}\) + \(\dfrac{1}{7}\) - \(\dfrac{1}{9}\) + \(\dfrac{1}{11}\) +...+ \(\dfrac{1}{87}\) - \(\dfrac{1}{89}\))
A = \(\dfrac{1}{2}\) \(\times\) (\(\dfrac{1}{5}\) - \(\dfrac{1}{89}\))
A = \(\dfrac{1}{2}\) \(\times\) \(\dfrac{84}{445}\)
A = \(\dfrac{42}{445}\)
mới giải đucợ 1 vế nè. xem tạm nhé
đặt cái biểu thức là S đi ^^
ta có:
\(\frac{1}{\left(n+1\right)\sqrt{n}}=\frac{\sqrt{n}}{\left(n+1\right)n}=\sqrt{n}.\frac{1}{n\left(n+1\right)} =\sqrt{n}\left(\frac{1}{\sqrt{n}}+\frac{1}{\sqrt{n+1}}\right) .\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)\)
< \(\sqrt{n}.\left(\frac{1}{\sqrt{n}}+\frac{1}{\sqrt{n}}\right).\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)\)
=\(\sqrt{n}.\frac{2}{\sqrt{n}}.\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)=2.\left(\frac{1}{\sqrt{n}}-\frac{1}{\sqrt{n+1}}\right)=\frac{2}{\sqrt{n}}-\frac{2}{\sqrt{n+1}}\)
áp dụng ta được: \(\frac{1}{2\sqrt{1}}< \frac{2}{\sqrt{1}}-\frac{2}{\sqrt{2}}\)
\(\frac{1}{3\sqrt{2}}< \frac{2}{\sqrt{2}}-\frac{2}{\sqrt{2}}\)
...................................................
\(\frac{1}{2011\sqrt{2010}}< \frac{2}{\sqrt{2010}}-\frac{2}{\sqrt{2011}}\)
=> \(S< 2-\frac{2}{\sqrt{2011}}< \frac{88}{45}\)
còn một vế nữa để mai nhé ^^ giờ mình bận :P hì
mình bị ấn sai r :3 \(\frac{1}{3\sqrt{2}}< \frac{2}{\sqrt{2}}-\frac{2}{\sqrt{3}}\)đó nhá.sr nha ^^