/ Cho tam giác ABC cân tại A có đường trung tuyến AM . Chứng minh tam giác ABM = tam giác ACM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2019
a,XétΔABM và ΔACM có :
^AMB=^AMC(=90o)
AB=AC(GT)
AM :cạnh chung(gt)
Suy ra:ΔABM= ΔACM (ch-cgv)
=>MB=MC( 2 cạnh tương ứng)
b,Ta có MB=BC2 =242 = 12
Δ AMB vuông tại M có :
AM2+BM2=AB2 ( đl Pytago)
=>AM2=AB2−BM2
= 202−122
= 162
=>AM=16
30 tháng 3 2021
a) Xét ΔABM vuông tại B và ΔACM vuông tại M có
AM chung
AB=AC(ΔABC cân tại A)
Do đó: ΔABM=ΔACM(cạnh huyền-cạnh góc vuông)
26 tháng 6 2023
a: M là trung điểm của BC
=>AM là đường trung tuyến của ΔABC
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
c: Sửa đề; tam giác ABC
AB=AC
BM=CM
=>AM là trung trực của BC
25 tháng 8 2021
vì tam giác ABC cân-> AB=AC
do M là trung điểm của BC-> MB=MC
xét tam giác ABM và tam giác ACM có:
AB=AC(cmt)
BM=MC(cmt)
cạnh AM chung
->tam giác ABM=tam giác ACM(c.c.c)
25 tháng 8 2021
Xét \(\Delta ABM\) và \(\Delta ACM\) có:
AB = AC (\(\Delta ABC\) cân)
\(\widehat{ABM}=\widehat{ACM}\)(\(\Delta ABC\) cân)
BM = CM (trung điểm M)
\(\Rightarrow\Delta ABM=\Delta ACM\)
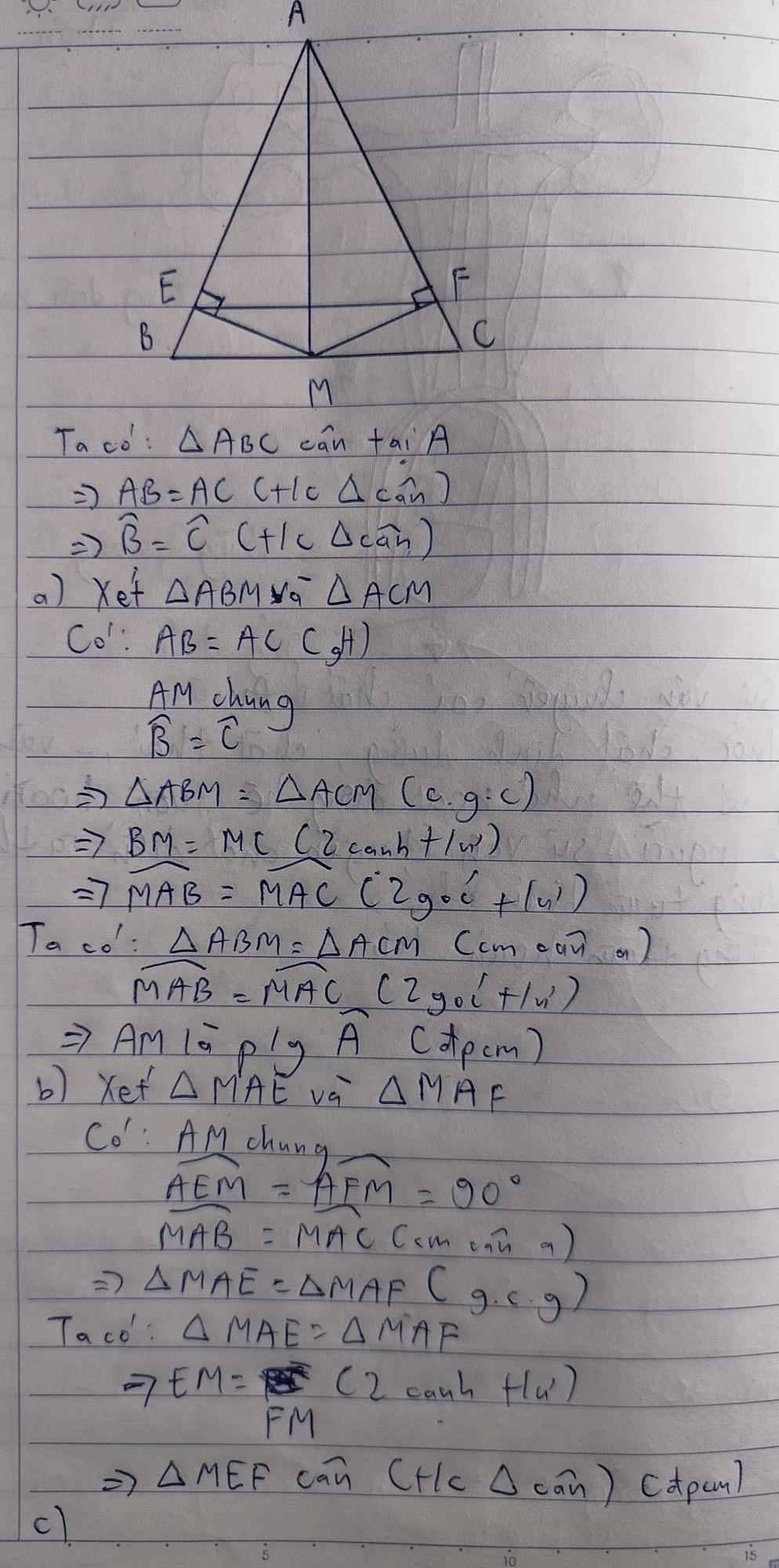
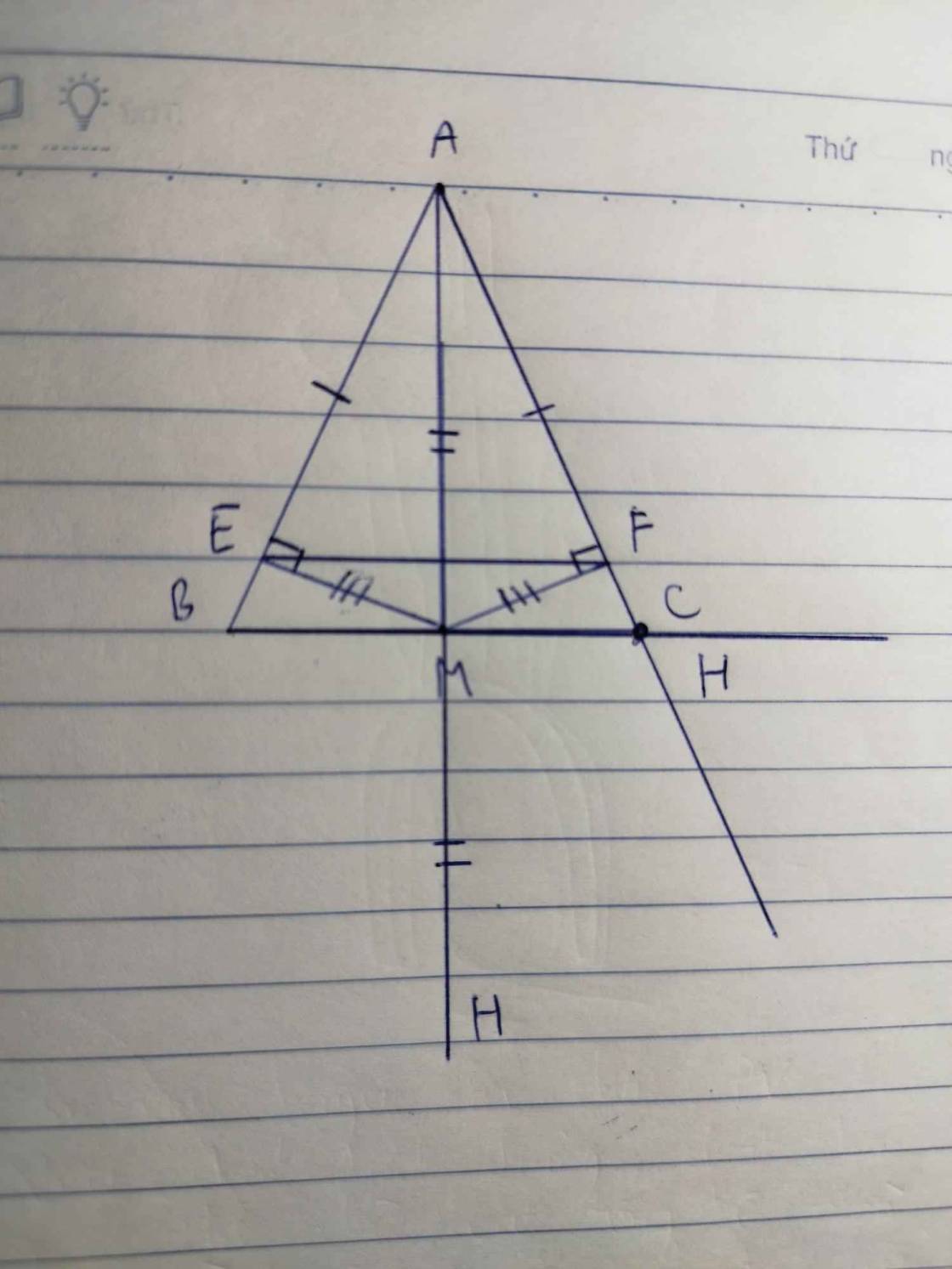
chỉ mình vs Mn ơiii
xét tam giác ABM và tam giác ACM ta có
AM=AM ( cạnh chung)
AB=AC( tam giác ABC cân tại A)
goc MAB = góc MAC ( AM là tia p.g góc BAC)
->tam giac ABM= tam giac ACM (c-g-c)