Ba đường thẳng phân biệt xy,mn,zt cùng đi qua điểm O và tạo thành các góc zOx = 38 độ C, tOm =71 độ C
a) Đọc tên các cặp góc đối đỉnh có trong hình đó
b) Cho biết số đo của các góc còn lại có trong hình đó
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
8 tháng 8 2019
a, Các cặp góc đối đỉnh là : xOz và tOy ; xOn và mOy ; zOn và tOm ; xOm và nOy ; xOt và zOy ; mOz và tOn ; các góc bẹt như tOz,yOx,nOm có góc đối đỉnh là chính nó.
b, Từ các cặp góc đối đỉnh suy ra ngay :
\(\widehat{zOx}=\widehat{tOy}=38^0,\widehat{tOm}=\widehat{zOn}=71^0\)
Từ tOz là góc bẹt suy ra :
\(\widehat{xOm}=180^0-\left[71^0+38^0\right]=71^0\)
Từ đó \(\widehat{xOm}=\widehat{yOn}=71^0\)
Các góc bẹt như tOz,yOx,nOm đều có số đo là 1800
CM
19 tháng 9 2018
Từ các cặp góc đối đỉnh suy ra ngay:
∠zOx = ∠tOy = 38°, ∠tOm = ∠zOn = 71°.
KT
27 tháng 9 2018
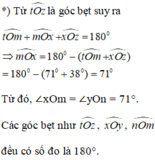
a) Vì \(MOP-MOQ\) là hai góc kề bù, ta có :
\(MOQ=180^0_{ }-MOP=180^0_{ }-70^0_{ }\)
\(\Rightarrow MOQ=110^0_{ }\)
Áp dụng tính chất hai góc đối đỉnh, ta có :
\(MOP=NOQ\)
\(MOQ=PON\)
b) Vì \(Ot\) là tia phân giác của \(MOP\Rightarrow TOP=TOM=\frac{1}{2}MOP=\frac{110}{2}=55^0_{ }\)
Vì \(POT-QOT'\) là hai góc đối đỉnh \(\Rightarrow POT=QOT'=55^0_{ }\left(1\right)\)
Vì \(MOT-NOT'\)là hai góc đối đỉnh \(\Rightarrow MOT=NOT'=55^0_{ }\left(2\right)\)
Từ \(\left(1\right)-\left(2\right)\Rightarrow OT'\)là tia phân giác của \(NOQ\)
c) \(POT-QOT'\)
\(MOT-NOT'\)
\(POM-NOQ\)