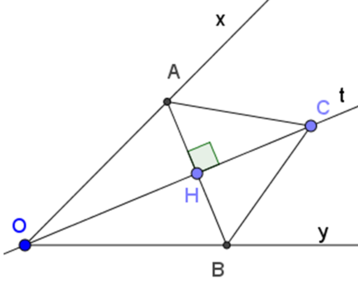
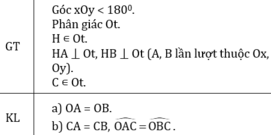
cho góc xOy khác góc bẹt . Ot là phân giác của góc đó . Qua điểm H thuộc tia Ot , kẻ đường vuông góc với Ot , nó cắt Õ và Oy theo thứ tự là A và B.
a) Chứng minh rằng OA=OB
b) Lấy điểm C thuộc tia Ot , chứng minh rằng CA=CB và góc OAC=OBC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 2 2021
a) Xét ΔAOH vuông tại H và ΔBOH vuông tại H có
OH chung
\(\widehat{AOH}=\widehat{BOH}\)(OH là tia phân giác của \(\widehat{AOB}\))
Do đó: ΔAOH=ΔBOH(cạnh góc vuông-góc nhọn kề)
Suy ra: OA=OB(Hai cạnh tương ứng)
b) Xét ΔCAO và ΔCBO có
OA=OB(cmt)
\(\widehat{AOC}=\widehat{BOC}\)(OC là tia phân giác của \(\widehat{AOB}\))
OC chung
Do đó: ΔCAO=ΔCBO(c-g-c)
Suy ra: CA=CB(hai cạnh tương ứng) và \(\widehat{OAC}=\widehat{OBC}\)(hai góc tương ứng)
LP
9 tháng 1 2022
a) ∆AOH và ∆BOH có:
ˆAOH=ˆBOH (gt) OH là cạnh chung
∆AOH =∆BOH( g.c.g)
Vậy OA=OB.
b) ∆AOC và ∆BOC có:
OA=OB (cmt)
ˆOAC = ˆOAB (gt)
OC cạnh chung.
Nên ∆AOC= ∆BOC(g.c.g)
Suy ra: CA=CB (hai cạnh tương ứng)
ˆOAC= ˆOBC ( góc tương ứng).
11 tháng 11 2016
a)
xét \(\Delta AHO\) và \(\Delta BHO\) có:
OH(chung)
\(\widehat{AHO}=\widehat{BHO}=90^o\)
\(\widehat{O_1}=\widehat{O_2}\left(gt\right)\)
\(\Rightarrow\Delta AHO=\Delta BHO\left(g.c.g\right)\)
=> OA=OB
b)
xét \(\Delta ACO\) và \(\Delta BCO\) có:
OA=OB(theo câu a)
\(\widehat{O_1}=\widehat{O_2}\)(gt)
OC(chung)
=>\(\Delta ACO=\Delta ABO\left(c.g.c\right)\)
=>\(\begin{cases}\widehat{OAC}=\widehat{OBC}\\CA=CB\end{cases}\)
16 tháng 7 2017
a) ∆AOH và ∆BOH có:=
(gt)
OH là cạnh chung
∆AOH =∆BOH( g.c.g)
Vậy OA=OB.
b) ∆AOC và ∆BOC có:
OA=OB(cmt)
=
(gt)
OC cạnh chung.
Nên ∆AOC= ∆BOC(g.c.g)
Suy ra: CA=CB(cạnh tương ứng)
=
( góc tương ứng).
CM
5 tháng 7 2017
ΔAOC và ΔBOC có:
OA = OB (cmt)
∠ AOC = ∠ BOC (vì Ot là tia phân giác góc xOy)
OC cạnh chung
⇒ ΔAOC = ΔBOC (c.g.c)
⇒ CA = CB (hai cạnh tương ứng)
∠ OAC = ∠ OBC ( hai góc tương ứng).
CM
18 tháng 3 2017
ΔAOH và ΔBOH có
∠ AOH = ∠ BOH (vì Ot là tia phân giác góc xOy)
OH cạnh chung
∠ OHA = ∠ OHB (= 90º)
⇒ ΔAOH = ΔBOH (g.c.g)
⇒ OA = OB (hai cạnh tương ứng)
4 tháng 12 2015
tự vẽ hình
a) Xét \(\Delta\)HAO vuông tại H và \(\Delta\)HBO vuông tại H
có : OH chung ; gócHOA =gócHOB ( Ot : phân giác)
=> \(\Delta\)HAO =\(\Delta\)HBO ( cạnh góc vuông - góc nhọn)
=> OA =OB ( cạnh tương ứng)
b) Xét \(\Delta\)CAO và \(\Delta\)CBO
có OA =OB ( cm trên)
gócCOA =góc COB
OC chung
=>\(\Delta\)CAO =\(\Delta\)CBO ( c-g-c)
=> góc OAC = góc OBC ( góc tương ứng)