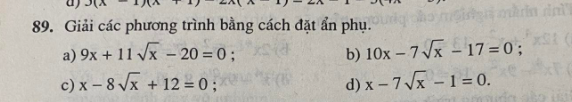
Giải hộ mình phần c,d nha thanks
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 11 2021
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}=\dfrac{x+y+z}{a+b+c}=\dfrac{x+y+z}{1}=x+y+z\)
\(\Rightarrow\dfrac{x^2}{a^2}=\dfrac{y^2}{b^2}=\dfrac{z^2}{c^2}=\left(x+y+z\right)^2\) (1)
\(\dfrac{x}{a}=\dfrac{y}{b}=\dfrac{z}{c}\Rightarrow\dfrac{x^2}{a^2}=\dfrac{y^2}{b^2}=\dfrac{z^2}{c^2}=\dfrac{x^2+y^2+z^2}{a^2+b^2+c^2}=\dfrac{x^2+y^2+z^2}{1}=x^2+y^2+z^2\) (2)
(1);(2) \(\Rightarrow\left(x+y+z\right)^2=x^2+y^2+z^2\)
25 tháng 1 2022
c: Để phương trình vô nghiệm thì \(\left(-2m\right)^2-4\left(m^2-m-1\right)< 0\)
=>4m+4<0
hay m<-1
HN
1
24 tháng 4 2021
Viên phấn càng ngắn càng khó bẻ đôi vì khi bẻ đôi viên phấn ta thường dùng đầu ngón tay làm điểm tựa tại vị trí mong muốn . Tuy nhiên khi viên phấn càng ngắn thì khoảng cách từ điểm tựa đến điểm tác dụng lực càng ngắn cho nên ta phải dùng một lực lớn hơn để bẻ viên phấn. Do đó việc bẻ đôi viên phấn sẽ khó
HL
1
LQ
5
30 tháng 3 2018
2x^2 - 3 = 29
=>2x^2 = 29 +3 = 32
=> x^2 = \(\frac{32}{12}\)=16
x=\(\sqrt{16}\)=4
vậy x = 4
LK
3
19 tháng 10 2015
sai đề không bé hơn 2005 có nghĩa là 2006,2007,........................
=> kết luận vô số
coi lại đề
c: \(\Leftrightarrow\left(\sqrt{x}-2\right)\cdot\left(\sqrt{x}-6\right)=0\)
=>x=4 hoặc x=36
d: Đặt \(\sqrt{x}=a\)
Pt sẽ là \(a^2-a-7=0\)
\(\text{Δ}=\left(-1\right)^2-4\cdot1\cdot\left(-7\right)=29>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}a_1=\dfrac{1-\sqrt{29}}{2}\left(loại\right)\\a_2=\dfrac{1+\sqrt{29}}{2}\left(nhận\right)\end{matrix}\right.\)
\(\Leftrightarrow\sqrt{x}=\dfrac{\sqrt{29}+1}{2}\)
hay \(x=\dfrac{30+2\sqrt{29}}{4}=\dfrac{15+\sqrt{29}}{2}\)
c) Đặt \(\sqrt{x}=a\left(a\ge0\right)\)
Ta có PT
\(a^2-8a+12=0\)
\(\Delta=\left(-8\right)^2-4.12=64-48=16>0\)
PT có 2 nghiệm phân biệt
\(\left[{}\begin{matrix}a_1=\dfrac{8+\sqrt{16}}{2}=\dfrac{12}{2}=6\\a_2=\dfrac{8-\sqrt{16}}{2}=\dfrac{4}{2}=2\end{matrix}\right.\)
Ta có
Với a = 6 thì \(\sqrt{x}=6\Leftrightarrow x=36\left(tm\right)\)
Với a = 2 thì \(\sqrt{x}=2\Leftrightarrow x=4\left(tm\right)\)