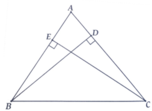
Cho tam giác nhọn ABC, hai đường cao BD và CE, Sade = 3/4 Sabc. Tính Â
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 8 2023
Xét tứ giác BEDC có
góc BEC=góc BDC=90 độ
=>BEDC là tứ giác nội tiếp
=>góc AED=góc ACB
Xét ΔAED và ΔACB có
góc AED=góc ACB
góc A chung
=>ΔAED đồng dạng với ΔACB
=>S AED/S ACB=(AE/AC)^2=(cos60)^2=1/4
=>S AED=1/4*S ACB
CM
23 tháng 9 2019
Ta có: ∆ABD ~ ∆ACE( g.g) => A D A B = A E A C
=> S A D E S A B C = A E A C 2
Mà trong ∆ACE có cosA = A E A C
=> S A D E S A B C = cos A 2
=> S A D E = S A B C . cos 2 A
22 tháng 4 2023
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AB*AE;AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
=>góc ADE=góc ABC
d: ΔADE đồng dạngvới ΔABC
=>\(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{ADE}=30\left(cm^2\right)\)
3 tháng 9 2021
c, Xét tam giác ADB vuông tại D có :
cosA = \(\frac{AD}{AB}=\frac{1}{2}\)
Lại có tam giác AED ~ tam giác ACB
\(\Rightarrow\frac{S_{ADE}}{S_{ABC}}=\left(\frac{AD}{AB}\right)^2\Rightarrow\frac{S_{ADE}}{12}=\frac{1}{4}\Rightarrow S_{ADE}=3\)cm2
10 tháng 5 2023
a: Xét ΔAFB vuông tại F và ΔAEC vuông tại E có
góc A chung
=>ΔAFB đồng dạng với ΔAEC
=>AF/AE=AB/AC
=>AF*AC=AB*AE
b: Xét ΔAFE và ΔABC có
AF/AB=AE/AC
góc A chung
=>ΔAFE đồng dạng với ΔABC
c: \(\dfrac{S_{AFE}}{S_{ABC}}=\left(\dfrac{AF}{AB}\right)^2=\dfrac{1}{4}\)
=>\(S_{AFE}=25\left(cm^2\right)\)
TA CÓ \(\Delta ADB\)đồng dạng \(\Delta AEC\)(g-g)
\(\Rightarrow\)\(\frac{AD}{AB}=\frac{AE}{AC}\)
Xét \(\Delta AED\)và \(\Delta ACB\) có :
góc A chung
\(\frac{AD}{AB}=\frac{AE}{AC}\)(CMT)
\(\Rightarrow\Delta AED\infty\Delta ACB\)(c-g-c)
\(\frac{S\Delta AED}{S\Delta ACB}=\left(\frac{AD}{AB}\right)^2\)=\(\frac{3}{4}\)
\(\Rightarrow\frac{AD}{AB}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\cos A=\frac{\sqrt{3}}{2}\)
\(\Rightarrow\)góc A=60 ĐỘ
cảm ơn bạn nhiều nha!!!!!!!!!!!!!!!!