vật sáng ab nằm trước thấu kính và cách thấu khính 18cm cho of=of' =9cm, ab=3cm. xác định o'a' và a'b'
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
27 tháng 3 2017
Sơ đồ tạo ảnh:
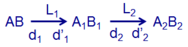
a) Ta có: d 1 ' = d 1 f 1 d 1 - f 1 = - 9 c m ; d 2 = l - d 1 ' = l + 9 ; d 2 ' = d 2 f 2 d 2 - f 2 = 24 ( l + 9 ) l - 15 .
Để ảnh cuối cùng là ảnh thật thì d 2 ' > 0 ⇒ 15 > l > 0 .
b) Ta có: d 1 ' = d 1 f 1 d 1 - f 1 = - 18 d 1 d 1 + 18 ; d 2 = l - d 1 ' = l d 1 + 18 l + 18 d 1 d 1 + 18 ;
d 2 ' = d 2 f 2 d 2 - f 2 = 24 ( l d 1 + 18 l + 18 d 1 ) l d 1 + 18 l - 6 d 1 - 432 ;
k = d 1 ' d 2 ' d 1 d 2 = - 432 l d 1 + 18 l - 6 d 1 - 432 = - 432 d 1 ( l - 6 ) + 18 l - 432 .
Để k không phụ thuộc vào d 1 thì l = 6 cm; khi đó thì k = 4 3 ; ảnh cùng chiều với vật.
H9
HT.Phong (9A5)
CTVHS
4 tháng 5 2023
Áp dụng công thức tính thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\)
\(\Rightarrow d'=\dfrac{d.f}{d-f}=\dfrac{9.3}{9-3}=4,5\left(cm\right)\)
Khoảng cách từ ảnh đến thấu kính là 4,5(cm)
Vậy khoảng cách từ ảnh đến vật là:
\(\Rightarrow d'+d=4,5+9=13,5\left(cm\right)\)
24 tháng 4 2021
a. Dựng ảnh A'B'
b) d > f , ảnh lớn hơn và ngược chiều với vật
c)
Tóm tắt:
OF = 12cm
OA = 18cm
AB = 6cm
A'B' = ?
Giải:
Δ ABF ~ OIF
\(\Rightarrow\dfrac{AB}{OI}=\dfrac{AF}{OF}\Leftrightarrow\dfrac{AB}{A'B'}=\dfrac{OA-OF}{OF}\Leftrightarrow\dfrac{6}{A'B'}=\dfrac{18-12}{12}\)
=> A'B' = 12cm
9 tháng 4 2022
Ảnh thật,ngược chiều và lớn hơn vật.
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{20}=\dfrac{1}{30}+\dfrac{1}{d'}\Rightarrow d'=60cm\)
Chiều cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}\Rightarrow\dfrac{3}{h'}=\dfrac{30}{60}\Rightarrow h'=6cm\)
30 tháng 3 2022
Khoảng cách từ ảnh đến thấu kính:
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Rightarrow\dfrac{1}{18}=\dfrac{1}{36}+\dfrac{1}{d'}\)
\(\Rightarrow d'=36cm\)
Độ cao ảnh:
\(\dfrac{h}{h'}=\dfrac{d}{d'}=\dfrac{36}{36}=1\Rightarrow h'=h=9cm\)