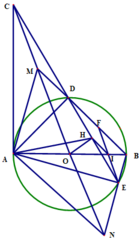
CHo (O:R) và điểm E cố điịnh nằm ngoài (O) .Vẽ đường thẳng đi qua O và E cắt (O) tại A và B sao cho A nằm giữa O và E .tia Ẽ di động cắt (O) tại M và N(M nằm giữa E và N).Chứng minh
1) EA.EB=EO2-R2
2) tam giác EAN đồng dạng tam giác EMB và viết tỉ số đồng dạng
3) EM.EN=OM2-R2