Câu 1 (2đ):Thời gian giải một bài toán (tính theo phút) của 30 học sinh được ghi lại trong bảng dưới đây:857897891286777987612887799796512a/ Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?b/ Lập bảng “tần số” .c/ Tính số trung bình cộng (làm tròn một chữ số thập phân)Câu 2(3đ): Cho hai đa thức f(x) = 5 +3x2 – x - 2x2 và g(x) = 3x + 3 – x – x2 a/ Thu gọn và sắp xếp hai đa thức theo lũy thừa giảm dần của biến.b/ Tính...
Đọc tiếp
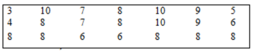
Câu 1 (2đ):Thời gian giải một bài toán (tính theo phút) của 30 học sinh được ghi lại trong bảng dưới đây:
8 | 5 | 7 | 8 | 9 | 7 | 8 | 9 | 12 | 8 |
6 | 7 | 7 | 7 | 9 | 8 | 7 | 6 | 12 | 8 |
8 | 7 | 7 | 9 | 9 | 7 | 9 | 6 | 5 | 12 |
a/ Dấu hiệu ở đây là gì? Số các giá trị là bao nhiêu?
b/ Lập bảng “tần số” .
c/ Tính số trung bình cộng (làm tròn một chữ số thập phân)
Câu 2(3đ): Cho hai đa thức f(x) = 5 +3x2 – x - 2x2 và g(x) = 3x + 3 – x – x2
a/ Thu gọn và sắp xếp hai đa thức theo lũy thừa giảm dần của biến.
b/ Tính h(x) = f(x) + g(x).
Câu 3(1đ): Tìm nghiệm của đa thức A(x) = x2 – 4x
Câu 4(3đ): Cho tam giác ABC nhọn và cân tại A, đường cao AH (H∈BC).
a/ Hai tam giác ABH và ACH có bằng nhau không? Vì sao?
b/ Tia AH có phải là tia phân giác của góc BAC không? Vì sao?
c/ Kẻ tia phân giác BK (K ∈ AC) của góc ABC. Gọi O là giao điểm của AH và BK. Chứng minh rằng CO là tia phân giác của góc ACB.

.png)
