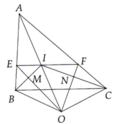
Cho tam giác ABC kẻ trung tuyến BE và CF cát nhau tại O. N,M lần lượt là trung điểm của OB và OC. Chứng minh È=MN,È song song vs MN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
13 tháng 7 2017
Cách 1: Sử dụng tính chất đường trung bình:
N là trung điểm của AB và M là trung điểm của AC => MN là đường trung bình của \(\Delta\)ABC.
=> MN//BC và MN=1/2BC (1)
I là trung điểm BG và K là trung điểm CG => IK là đường trung bình của \(\Delta\)BGC.
=> IK//BC và IK=1/2BC (2)
Từ (1); (2) => MN//IK và MN=IK (đpcm)
Cách 2: Chứng minh 2 tam giác bằng nhau:
G là trọng tâm của \(\Delta\)ABC => BG=2GM và CG=2GN.
Mả I là trung điểm của BG => BI=GI=GM
K là trung điểm của CG => CK=GK=GN
Xét \(\Delta\)IGK và \(\Delta\)MGN:
GI=GM
^IGK=^MGN => \(\Delta\)IGK=\(\Delta\)MGN (c.g.c)
GK=GN
=> MN=IK (2 cạnh tương ứng) và ^GIK=^GMN => MN//IK (So le trong)
Cách 3: Sử dụng tính chất đoạn chắn đảo:
Ta có: \(\Delta\)NIG=\(\Delta\)KMG (c.g.c) => ^NIG=^KMG (So le trong) => NI//KM.
Mả NI=KM (2 cạnh tương ứng) => MN//IK và MN=IK (đpcm)
13 tháng 7 2017
xét tam giác BCG có I, K là trung điểm của BG, CG (gt)
=> IK là đường trung bình của tam giác
=> IK//BC và IK=1/2 BC (1)
xét tam giác ABC có M, N là trung điểm của AB, AC (đường trung tuyến)
=> MN là đường trung bình của tam giác
=> MN//BC và MN=1/2 BC (2)
từ (1) và (2) => MN//IK//BC và MN=IK=1/2BC
AD
4 tháng 8 2015
ta cm MN va PN cung vuong goc EF
mn la trung tuyen tam giac mef co me=mf =>mn vuong goc ef
tuong tu, xet tam giac pef ta cung co pn vuong goc ef
17 tháng 10 2019
Bạn vé hình giống của ((Me)) nhé ..
a, AB=AC (gt)
\(\Rightarrow\frac{1}{2}AB=\frac{1}{2}AC\Rightarrow\hept{\begin{cases}AN=AM\\CM=BN\end{cases}}\)
Xét 2 \(\Delta ABM\)và \(\Delta CAN\)có:
góc A chung
AB=AC(gt)
\(AN=AM\)( cmt)
\(\Rightarrow\Delta AMB=\Delta ACN\left(c.g.c\right)\)
Xét 2 \(\Delta BMC\)Và \(\Delta CNB\)Có:
Cạnh BC chung
Góc \(ABC\)= góc \(ACB\)
\(BN=CM\)(Cmt)
\(\Rightarrow\Delta NBC=\Delta MCB\left(c.g.c\right)\)
Từ A Kẻ \(AK\perp BC\)
\(\Rightarrow\)AK là đường phân giác của \(\Delta ABC\)(Vì \(\Delta ABC\)Là tam giác cân )
\(\Rightarrow NAK=KAC\)
gọI O là gia điểm của hai đường chéo CF và BE
Xét 2 \(\Delta ANO\)Và \(\Delta AMO\)Có :
Góc \(NAO\)= Góc \(MAO\)(Cmt)
Cạnh \(AO\)Chung
\(AN=AM\)(Theo câu a)
\(\Rightarrow\Delta ANO=\Delta AMO\left(C.g.c\right)\)
\(\Rightarrow ANO=AMO\)(Cặp góc tương ứng )
Ta có : góc \(FNA+ANO=180^O\)(Cặp góc kề bù )
góc \(EMA+AMO=180^O\)(Cặp góc kề bù )
Mà góc \(ANO=AMO\)(Cmt)
\(\Rightarrow EMA=FNA\)
vÌ \(\Delta ABC\)Cân và N ,M lần lượt là trung điểm của AB,AC
\(\Rightarrow CN=BM\)
\(\Rightarrow NF=ME\)
xÉT 2 \(\Delta AFN\)VÀ \(\Delta AEM\)có :
góc \(ANF=EMA\)(Cmt)
\(AM=AN\)(Cmt)
\(FN=ME\)(Cmt)
\(\Rightarrow\DeltaÀFN=\Delta AEM\left(C.g.c\right)\)
\(\Rightarrow AF=AE\)(CẶP CẠNH TƯƠNG ỨNG )
\(\Rightarrow A\)Là trung điểm của EF
Lấy I là gia điểm của NM và AK
Vì \(\Delta ABC\)là tam giác cân
\(\Rightarrow AK\)\(\perp MN\)
Ta có : \(\hept{\begin{cases}MN\perp AK\\BC\perp AK\end{cases}}\Rightarrow MN\)// \(BC\)(Tính chất từ vuông góc đến song song)
TT
4 tháng 8 2020
câu a CHỨNG Minh AB = DC CHỨ sao AB = BC ĐC
A) XÉT \(\Delta ABC\)VÀ \(\Delta CDA\)CÓ
\(\widehat{ACB}=\widehat{CAD}\)( VÌ AD // BC , HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG )
AC LÀ CẠNH CHUNG
\(\widehat{BAC}=\widehat{DCA}\)( VÌ AB // DC , HAI GÓC NÀY Ở VỊ TRÍ SO LE TRONG )
=> \(\Delta ABC=\Delta CDA\left(g-c-g\right)\)
=> AD = BC (HAI CẠNH TƯƠNG ỨNG )
=> AB = DC ( HAI CẠNH TƯƠNG ỨNG )
TA CÓ M LÀ TRUNG ĐIỂM CỦA BC
\(\Rightarrow BM=CM=\frac{BC}{2}\left(1\right)\)
TA CÓ N LÀ TRUNG ĐIỂM CỦA AD
\(\Rightarrow AN=DN=\frac{AD}{2}\left(2\right)\)
TỪ (1) VÀ (2)
\(BM=CM=\frac{BC}{2}\)
\(AN=DN=\frac{AD}{2}\)
MÀ AD = BC ( CMT)
=> \(BM=CM=AN=DN\)
XÉT \(\Delta BAM\)VÀ \(\Delta DCN\)CÓ
\(BA=DC\)(VÌ \(\Delta ABC=\Delta CDA\))
\(\widehat{ABM}=\widehat{CDN}\)(VÌ \(\Delta ABC=\Delta CDA\))
\(BM=DN\left(cmt\right)\)
=>\(\Delta BAM=\Delta DCN\left(c-g-c\right)\)
=> AM = CN (HAI CẠNH TƯƠNG ỨNG )
c) XÉT TỨ GIÁC ABCD
ta có \(AD=BC\left(cmt\right);AB=CD\left(cmt\right)\)
=> TỨ GIÁC ABCD LÀ HÌNH THOI
=> CÁC ĐƯỜNG CHÉO CẮT NHAU TẠI TRUNG ĐIỂM CỦA NÓ
=> \(OA=OC;OB=OD\)
5 tháng 8 2020
mượn hình của Lê Trí Tiên làm tiếp câu (d)
vì M là trung điểm AD và O là trung điểm của AC => ON là đường trung bình tam giác ACD
=> ON //DC (1)
chứng minh tương tự ta có: OM là đường trung bình tam giác ACB
=> OM // AB mà AB // CD => OM // DC (2)
từ (1) (2) => M,O,N thằng hàng (đpcm)