Mọi người giải giúp em câu này với ạ em cần ngay trong ngay mai ạ 
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn cần bài nào ạ? Nếu bạn cần giúp tất cả thì bạn tách ra từng CH khác nhau nhé!

Lời giải:
$\frac{x-2y}{3z}$ có thể nhận giá trị lớn nhất nếu $x$ lớn nhất và $y,z$ nhỏ nhất có thể.
$x$ lớn nhất có thể nhận là $14$ (theo điều kiện)
$y,z$ nhỏ nhất có thể nhận là $1,2$ (do $y,z$ phân biệt)
Nếu $x=14, y=1,z=2$ thì $\frac{x-2y}{3z}=2$
Nếu $x=14; y=2, z=1$ thì $\frac{x-2y}{3z}=\frac{10}{3}>2$
Đáp án D.

bài này mk bt lm nhưng mk đag trog trạng thái mệt mỏi nên ngại lắm, để lúc nào rảnh mk giúp bn nhé!

vẽ lại mạch ta có RAM//RMN//RNB
đặt theo thứ tự 3 R là a,b,c
ta có a+b+c=1 (1)
điện trở tương đương \(\dfrac{1}{R_{td}}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\) \(\Rightarrow I=\dfrac{U}{R_{td}}=9.\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\) với a,b,c>0
áp dụng bất đẳng thức cô si cho \(\dfrac{1}{a},\dfrac{1}{b},\dfrac{1}{c}\) \(\Rightarrow\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\ge\dfrac{3}{\sqrt[3]{abc}}\ge\dfrac{3}{\left(\dfrac{a+b+c}{3}\right)}=\dfrac{9}{a+b+c}=9\)
\(\Leftrightarrow9\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)\ge81\Leftrightarrow I\ge81\) I min =81 ( úi dồi ôi O_o hơi to mà vẫn đúng đá nhỉ)
dấu ''='' xảy ra \(\Leftrightarrow a=b=c\left(2\right)\)
từ (1) (2) \(\Rightarrow a=b=c=\dfrac{1}{3}\left(\Omega\right)\)
vậy ... (V LUN MẤT CẢ BUỔI TỐI R BÀI KHÓ QUÁ EM ĐANG ÔN HSG À )

a) \(\dfrac{A}{x-2}=\dfrac{x^2+3x+2}{x^2-4}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{\left(x+2\right)\left(x+1\right)}{\left(x-2\right)\left(x+2\right)}\)
\(\Leftrightarrow\dfrac{A}{x-2}=\dfrac{x+1}{x-2}\Leftrightarrow A=x+1\)
b) \(\dfrac{M}{x-1}=\dfrac{x^2+3x+2}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=\dfrac{\left(x+1\right)\left(x+2\right)}{x+1}\)
\(\Leftrightarrow\dfrac{M}{x-1}=x+2\Leftrightarrow M=\left(x-1\right)\left(x+2\right)=x^2+x-2\)

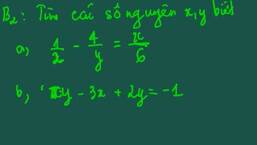


 mọi người giải giúp em bài này với ạ em đang cần gấp ạ
mọi người giải giúp em bài này với ạ em đang cần gấp ạ


 Mọi người giúp em câu này gấp với ạ, sáng mai em phải trả bài rồi. Em cảm ơn mọi người rất nhiều!
Mọi người giúp em câu này gấp với ạ, sáng mai em phải trả bài rồi. Em cảm ơn mọi người rất nhiều!
a, An đã vi phạm nội quy của trường, lớp
=> Đạo đức của học sinh
Đồng thời, vi phạm luật giao thông ( do tham gia đua xe lạng lách đánh võng trên đường )
=> Đạo đức của người tham gia giao thông < Chắc thể :] >
b, Người có quyền xử lí những hành vi đó của An là:
- Bố mẹ
- Thầy cô giáo
hoặc có thể là cơ quan nhà nước ( cảnh sát giao thông )
c, Nếu là bạn cùng lớp với An thì em sẽ:
- Khuyên bạn nên chú tâm hơn vào học hành
- Không nên để ba mẹ buồn, phiền lòng về bản thân nữa
- Khi tham gia giao thông thì phải tuân thủ quy định
- Nêu những tác hại về việc chơi bời lêu lổng, không học hành để bạn tự xem lại chính mình và có ý chí phấn đấu hơn
- Nhờ các thầy cô giáo giúp đỡ bạn để bạn được tiến bộ hơn
- Đồng thời, nói chuyện với ba mẹ của bạn ấy để giúp bạn
Ý kiến riêng của mình, bạn có thể thêm vào ha!
a. An đã vi phạm nội quy của trường và đạo đức trách nhiệm trong cuộc sống
b. Thầy cô và nhà nước sẽ là người có quyền xử lí những hành vi vi phạm pháp luật của An
c. Em sẽ khuyên bn nên cố gắng học tập và ko ăn chơi nx